Polynôme à plusieurs indéterminées
Les polynômes comme :
sont des polynômes à une seule indéterminée qui est .
Un polynôme à deux indéterminées et serait par exemple :
Un polynôme à trois indéterminées , et serait par exemple :
et ainsi de suite..
Ces polynômes se présentent sous forme de somme de termes de la forme que l'on appelle monôme. Un polynôme est donc une somme de monômes.
Le degré d'un monôme est égal à la somme des puissances des indéterminées , , , etc.
Si tous les monômes du polynôme ont le même degré, on dit que le polynôme est homogène.
Par exemple :
est un polynôme homogène de degré 5.
Si nous avons dit cela, ce n'est pas pour faire un cours sur les polynômes, mais pour donner un premier conseil sur la transformation d'expressions algébriques.
Les expressions algébriques à transformer sont souvent faites de polynômes homogènes. Nous avons alors la règle suivante :
Lorsque l'on factorise un polynôme homogène en produit de polynômes homogènes, la somme des degrés de tous les facteurs sera égal au degré du polynôme homogène de départ.
|
|
Exemple. Dans l'identité remarquable :
on a : Au premier membre, un polynôme homogène à deux indéterminées et du second degré. Au second membre, un produit de deux polynômes homogènes à deux indéterminées et du premier degré. |
Astuce de factorisation
Nous commencerons par énoncer la règle suivante :
Soit une expression algébrique et soit une (sous-)expression algébrique apparaissant dans .
Si l'on réussit à trouver une expression telle que le fait de remplacer par dans permet de rendre nul, alors cela signifie que l'on peut mettre en facteur dans .
|
|
Exemple. Supposons que l'on doive factoriser l'expression :
nous remarquons qu'en remplaçant par , nous obtenons :
Nous pouvons donc commencer la factorisation ainsi :
étant une expression algébrique à déterminer. (nous verrons, dans la suite de cette leçon, plusieurs méthodes pour déterminer ) |
Monômes de plus haut degré uniques
Nous avons la règle suivante :
Soit un polynôme à plusieurs indéterminées et soit et deux polynômes vérifiant :
Alors et ont un monôme de plus haut degré unique si et seulement si a un monôme de plus haut degré unique.
Le produit du monôme de plus haut degré de par le monôme de plus haut degré de donnera alors le monôme de plus haut degré de .
|
|
Exemple. Poursuivons l'exemple du paragraphe précédent. Nous avons vu qu'il existe une expression algébrique vérifiant :
Il nous restait à déterminer . D'après la règle 3, on doit pouvoir écrire sous la forme :
et en reportant, on obtient :
qui se simplifie sous la forme :
Nous pouvons considérer que la situation s'est améliorée car nous avons maintenant au premier membre un polynôme de degré 4 (au lieu de 5). Réappliquons la règle 3. On doit pouvoir écrire sous la forme :
et en reportant, on obtient :
qui se simplifie sous la forme :
Où l'on voit clairement que :
Si l'on récapitule, on a :
En reportant dans :
nous pouvons conclure que : |
Monômes de plus haut degré multiples
La méthode utilisée dans l'exemple du paragraphe précédent peut se généraliser à des polynômes où il y a plusieurs monômes du degré le plus élevé. Dans ce cas-là, on risque de s'y prendre à plusieurs reprises pour savoir quel monôme doit être divisé par tel ou tel monôme. On tentera alors de faire en sorte qu'après simplification le degré du polynôme du premier membre diminue et que le nombre de monômes dans le premier membre se réduise.
Pour ce faire, une méthode qui permet souvent d'aboutir est de commencer par rechercher tous les quotients possibles en divisant tous les monômes de plus haut degré du premier membre par tous les monômes de plus haut degré apparaissant dans le second membre et de choisir le ou les quotients qui apparaissent le plus souvent.
C'est pas très clair, prenons un exemple :
|
|
Exemple. Supposons que l'on doivent déterminer un polynôme tel que :
Nous sommes dans le cas le plus défavorable car les deux polynômes en présence sont tous les deux homogènes. Les monômes présents sont donc tous de plus haut degré. Le quotient du monôme du premier membre par le monôme du second membre donne le monôme . Le quotient du monôme du premier membre par le monôme n'est pas possible. Le quotient du monôme du premier membre par le monôme du second membre donne le monôme . Le quotient du monôme du premier membre par le monôme n'est pas possible. Le quotient du monôme du premier membre par le monôme du second membre donne le monôme . Le quotient du monôme du premier membre par le monôme du second membre donne le monôme . Le quotient du monôme du premier membre par le monôme n'est pas possible. Le quotient du monôme du premier membre par le monôme du second membre donne le monôme . Le quotient du monôme du premier membre par le monôme du second membre donne le monôme . Le quotient du monôme du premier membre par le monôme du second membre donne le monôme . Le quotient du monôme du premier membre par le monôme n'est pas possible. Le quotient du monôme du premier membre par le monôme n'est pas possible. Le quotient du monôme du premier membre par le monôme n'est pas possible. Le quotient du monôme du premier membre par le monôme du second membre donne le monôme . Le quotient du monôme du premier membre par le monôme n'est pas possible. Le quotient du monôme du premier membre par le monôme n'est pas possible. Le quotient du monôme du premier membre par le monôme n'est pas possible. Le quotient du monôme du premier membre par le monôme du second membre donne le monôme .
Nous considérerons donc que ces deux monômes ont une forte probabilité de figurer dans et nous poserons :
En remplaçant plus haut, on obtient :
qui se simplifie ainsi :
la situation s'est un peu améliorée car nous n'avons plus que 4 monômes au premier membre (au lieu de 6). et on recommence : Le quotient du monôme du premier membre par le monôme du second membre donne le monôme . Le quotient du monôme du premier membre par le monôme n'est pas possible. Le quotient du monôme du premier membre par le monôme du second membre donne le monôme . Le quotient du monôme du premier membre par le monôme du second membre donne le monôme . Le quotient du monôme du premier membre par le monôme du second membre donne le monôme . Le quotient du monôme du premier membre par le monôme n'est pas possible. Le quotient du monôme du premier membre par le monôme du second membre donne le monôme . Le quotient du monôme du premier membre par le monôme n'est pas possible. Le quotient du monôme du premier membre par le monôme du second membre donne le monôme . Le quotient du monôme du premier membre par le monôme du second membre donne le monôme . Le quotient du monôme du premier membre par le monôme n'est pas possible. Le quotient du monôme du premier membre par le monôme n'est pas possible.
Nous poserons donc :
Nous réservant par la suite la possibilité de choisir et de façon à minimiser le nombre de monômes du premier membre de l'expression :
qui se simplifie sous la forme :
Si l'on veut faire disparaître un maximum de monôme du premier membre, l'idéal serait que et satisfasse le système :
Nous voyons que l'on peut satisfaire trois équations en prenant :
Dans ce cas, on aura :
qui nous donnera :
et nous remarquons que l'on peut factoriser sous la forme :
Ce qui nous montre que :
Si l'on récapitule, on a :
En reportant dans :
on obtient finalement : |
Invariance par permutation circulaire
On dira qu'une expression est invariante par permutation circulaire des variables si en plaçant les variables sur un cercle, l'expression ne change pas en remplaçant chaque variable par celle qui suit en tournant dans le cercle (dans le même sens pour toutes les variables). L'expression devra rester invariante si l'on continue à tourner jusqu'à revenir à l'expression initiale.
Par exemple, considérons l'expression :
Plaçons les trois variables sur un cercle :
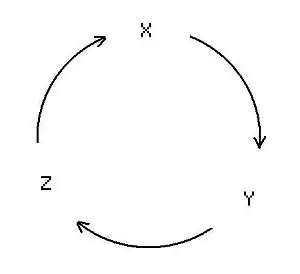
En tournant, par exemple dans le sens des aiguilles d'une montre, nous voyons que :
est remplacé par .
est remplacé par .
est remplacé par .
L'expression devient alors :
mais si l’on regarde bien, c'est toujours la même expression.
Si l'on continue à tourner, on obtient :
et c'est encore la même expression.
Si on continue à tourner encore une fois, on retombe sur l'expression de départ.
On a donc bien affaire à une expression invariante par permutation circulaire des variables , et .
Nous avons alors les deux règles suivantes :
Si une expression est invariante par permutation circulaire de certaines variables, alors elle reste invariante par permutation circulaire des mêmes variables après une transformation (simplification, factorisation, etc.) de cette expression.
C'est évident, mais si l'on prend la peine de le préciser, c'est parce que cette règle est utile, ne serait-ce que pour détecter des erreurs lorsque l'on transforme une expression invariante par permutation circulaire et que l'on constate que l'expression obtenue n'est plus invariante par permutation circulaire.
Soit une expression invariante par permutation circulaire de certaines variables.
Si l'on sait que dans cette expression, on peut mettre en facteur une expression particulière E qui n'est pas invariante par permutation circulaire des mêmes variables, alors on pourra aussi mettre en facteur toute expression obtenue par permutation circulaire des variables dans E.
|
|
Exemple. Soit à factoriser l'expression :
Nous voyons que cette expression est invariante par permutation circulaire des variables , et . Si l'on remplace par , nous voyons que l'expression s'annule. D'après la règle 2, on en déduit que l'on peut mettre en facteur. Mais n'est pas invariante par permutation circulaire des variables , et . D'après la règle 5, on en déduit que l'on peut aussi mettre en facteur les expressions obtenues par permutation circulaire des variables , et dans l'expression , c'est-à-dire et . Il existera donc une expression tel que :
Mais d'après la règle 1, on déduit que est un polynôme homogène de degré 0, c'est-à-dire une constante que l'on détermine facilement et qui est 1. On obtient donc finalement : |
Parité par rapport à une variable
Nous avons la définition suivante :
Une expression sera dite paire par rapport à une variable si le fait de transformer cette variable en son opposé ne change pas l'expression.
Une expression sera dite impaire par rapport à une variable si le fait de transformer cette variable en son opposé transforme l'expression en son opposé.
Par exemple l'expression :
est paire par rapport à et impaire par rapport à
La parité d'une expression par rapport à une variable ne change pas lors d'une transformation (simplification, factorisation, etc.) d'une expression.
Là aussi cette règle permet de détecter des erreurs si l'on constate que la parité par rapport à une variable n'est pas la même dans le résultat qu'au début.
Cette règle peut aussi permettre certaines opérations.
|
|
Exemple. Soit à simplifier l'expression :
Toute tentativespour factoriser le dénominateur pour faire apparaître un facteur qui pourrait aussi apparaître dans le numérateur semble vouée à l'échec. Toutefois si l'exercice a été posé c'est que le dénominateur en entier doit être un facteur du numérateur. Pour le vérifier, utilisons la règle 2 en remplaçant dans le numérateur par (c'est ce qui semble le plus simple). On obtient :
Il existe donc tel que :
et c'est là qu'intervient la règle 6. Nous voyons que le premier membre est pair par rapport à . Le second membre doit donc aussi être pair par rapport à . Si l'on transforme en , le second membre devient :
Cette expression devant toujours être égale à , nous en déduisons qu'il y a aussi en facteur.
En développant le second membre on voit que et donc :
Finalement, la simplification de l'expression de départ pourra s'effectuer ainsi : |
Polynôme symétrique
Un polynôme sera dit symétrique par rapport à certaines variables si une permutation quelconque de deux de ces variables laisse le polynôme inchangé. Si on ne précise pas les variables, c'est qu'il est symétrique par rapport à toutes les variables.
Par exemple :
est un polynôme symétrique.
est un polynôme symétrique par rapport aux variables et .
Un polynôme symétrique par rapport à certaines variables reste symétrique par rapport à ces variables lors d'une transformation (simplification, factorisation, etc.).