Définition de la continuité
Soit f une fonction définie sur un intervalle I et a un réel de I.
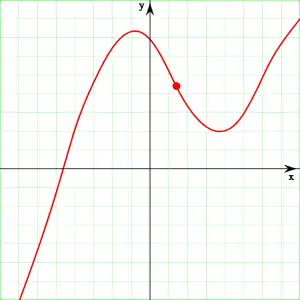
- f est continue en a si sa limite en a est égale à sa valeur en a:
- f est continue sur I si f est continue en tout a appartenant à I.
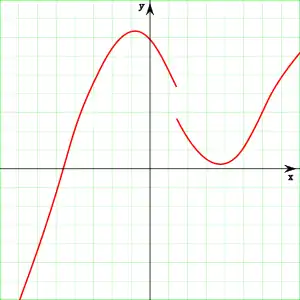
- Cette situation s'oppose à la suivante : une fonction f est discontinue en un point a si la courbe de f présente une "coupure" en x=a qui oblige à "lever le crayon" pour parcourir la courbe.
Continuité des fonctions usuelles
La dérivabilité est un critère utile de continuité pour les fonctions usuelles.
Soit f une fonction définie sur un intervalle I et a un réel de I.
Si f est dérivable en a alors f est continue en a.
Remarque:
- La réciproque est fausse : la fonction racine carrée est continue en 0 mais non dérivable en 0.
- Les fonctions polynômes, exponentielle, sinus et cosinus sont continues sur .
- Les sommes, différences, produits, quotients et composées des fonctions précédentes
sont continues sur les intervalles qui forment leur ensemble de définition.
Exemple
La fonction inverse est continue sur et est continue sur .
![]-\infty ;0[](../../I/dc1517caf3346855d4718b15e52608b9cc04760a.svg)
![]0;+\infty[](../../I/9a2b9afa8192cc3f8173fadddad0d1f5c499d881.svg)
Mais elle n’est pas continue sur car non définie sur tout entier.
De plus, cela n'a pas de sens pour nous de se demander si elle est continue sur
![{\displaystyle ]-\infty ;0[\cup ]0;+\infty [}](../../I/e6778831cc5166db4161c21ec85475528a7a79a4.svg)
car on n'a défini la continuité que sur un intervalle.
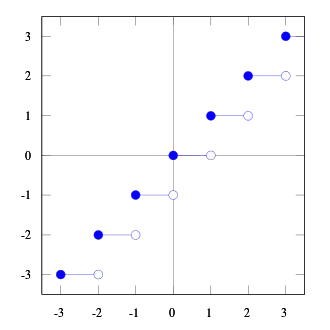
La fonction partie entière
La fonction partie entière est définie sur en remarquant que pour tout réel il existe un unique entier tel que : . Alors, .
Elle est continue en tout point non entier et discontinue en tout point entier.
