Nous allons voir dans ce chapitre quels sont les apports des nombres complexes à la trigonométrie et ils sont considérables. Si l’on ne considère pas les nombres complexes, beaucoup de formules sont difficiles à établir et à retenir. Les nombres complexes vont nous permettre, non seulement d'établir des formules trigonométriques que l’on avait eu bien du mal à établir par des raisonnements de géométrique euclidienne dans le cercle trigonométrique, mais en plus les nombres complexes vont nous permettre d’établir des nouvelles formules qu’il aurait été encore plus compliqué d’établir grâce à la géométrie euclidienne. On peut même se risquer à dire que l'élève ou l'étudiant, qui aura parfaitement compris ce chapitre, n'a plus besoin d'encombrer sa mémoire avec toutes les formules trigonométriques, car les nombres complexes vont lui permettre de les retrouver très rapidement et très simplement en cas de besoin.

Nombres complexes de module 1

Si l’on considère le plan complexe et que l’on regarde quels sont les points dont l'affixe est un nombre complexe de module 1, on voit aisément que c’est le cercle de rayon 1 centré sur l'origine du repère.

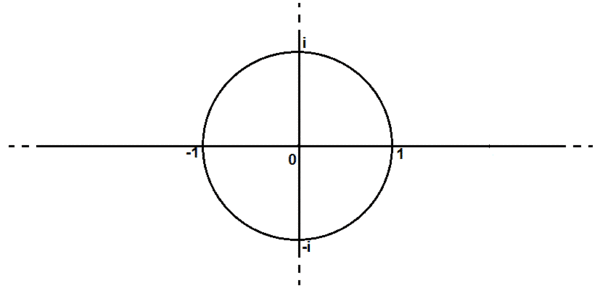
Nous savons que ce cercle porte un nom particulier, c’est le cercle trigonométrique. Nous avons vu que lorsqu'on multiplie deux nombres complexes, on multiplie leur module. Et comme tous les points du cercle trigonométrique ont pour affixe un nombre complexe de module 1 et que 1 fois 1 égale 1, le produit de deux nombres complexes du cercle trigonométrique donnera l'affixe d'un point du cercle trigonométrie. De même qu'en multipliant deux nombres de la droite réelle, on reste sur la droite réelle, en multipliant deux nombres du cercle trigonométrique, on reste sur le cercle trigonométrique.

Cette propriété remarquable du cercle trigonométrique, nous amène à étudier de plus près cet ensemble. En fait, si l’on se focalise sur le cercle trigonométrique, pour multiplier deux nombres complexes, il suffit d'ajouter leur argument. Et nous constatons une chose remarquable, c’est que pour le cercle trigonométrique, faire une multiplication des affixes revient à faire une addition de leur argument.

Si nous cherchons dans notre mémoire, nous avons déjà rencontré une situation où faire une multiplication revenait à faire une addition. Rappelez-vous de la formule :

${\displaystyle a^{n}\times a^{m}=a^{n+m}}$

Pour multiplier deux puissances, il faut ajouter leur exposant. Et là, une idée germe dans notre continuum mental : si multiplier deux nombres complexes de module 1 revient à ajouter leur argument, peut-être qu’il est possible de représenter un nombre complexe de module 1 par une puissance contenant l'argument dans l'exposant. si α est l'argument d'un nombre complexe, alors il existe peut-être un nombre « e » tel que le nombre complexe de module α s'écrive :

${\displaystyle e^{\alpha }}$

Des études plus approfondies montrent que cette formulation n’est pas assez générale et que l’on doit rajouter dans l'exposant une constante multiplicative proportionnelle au nombre i. On choisit e de telle façon que cette constante multiplicative soit exactement i.

Exponentielle complexe

Tout nombre complexe de module 1 et d'argument α s'écrit sous la forme :

${\displaystyle \mathrm {e} ^{\alpha \mathrm {i} }}$.

Me diriez-vous : N'a-t-on pas oublié, avant d'énoncer cette propriété, de déterminer la constante e ? Je vous répondrais que la valeur de cette constante ne sert à rien pour la suite de cette leçon. Comment ! vous insistez ? Très bien, pour les curieux, je dirais que c’est une des constantes fondamentales des mathématiques comme le nombre π qui vaut à peu près 3,14. Comment, vous voulez aussi la valeur de la constante e ? C’est bon, je vous la donne :

${\displaystyle \mathrm {e} =2{,}71828....}$

Comme π, il y a une infinité de chiffres après la virgule.

Bon ! Revenons à des choses pour l'instant plus utiles. Compte tenu de la définition, nous avons de façon immédiate :

Nous pouvons aussi, en donnant des valeurs particulières à α, obtenir quelques valeurs remarquables

La troisième des trois précédentes formules peut se mettre sous la forme :

Cette dernière formule, appelée l'identité d'Euler, est considérée par certains mathématiciens comme une œuvre d'art mathématique. En effet, elle donne une relation très simple entre les trois constantes les plus fondamentales des mathématiques, à savoir e, π et i.

Formule d'Euler

Toujours en restant dans le cercle trigonométrique, considérons les parties réelle et imaginaire des nombres complexes de module 1.

Nous avons vu dans le cours de trigonométrie que l'abscisse et l'ordonnée d'un point M du cercle trigonométrique s'exprime respectivement par le cosinus et le sinus de l'angle formé par la demi-droite portant les abscisses positives et la demie droite [OM). On en déduit immédiatement les mêmes relations pour les parties réelle et imaginaire de l'affixe du point M.

Si ${\displaystyle m}$ est l'affixe du point M, on peut alors écrire, d’après le chapitre précédent :

${\displaystyle m=\cos \alpha +\mathrm {i} \sin \alpha }$

Mais nous avons vu dans le paragraphe précédent que :

${\displaystyle m=\operatorname {e} ^{\alpha \mathrm {i} }}$

Nous en déduisons donc que :

${\displaystyle \operatorname {e} ^{\alpha \mathrm {i} }=\cos \alpha +\mathrm {i} \sin \alpha }$.

Cette relation est très importante. Elle est propre au nombre complexe et n'existait pas dans l’ensemble des nombres réels. Sa seule variable est l'angle α.

Relation d'Euler

Soit α, un angle. Cet angle vérifie la relation :

${\displaystyle \operatorname {e} ^{\alpha \mathrm {i} }=\cos \alpha +\mathrm {i} \sin \alpha }$,

qui est appelée relation d'Euler ou formule d'Euler.

Cette relation, comme nous allons le vérifier, permet de retrouver la quasi totalité des formules trigonométriques et d’en établir de nouvelles.

Notation exponentielle d'un nombre complexe

Nous avons vu au chapitre précédent la notation trigonométrique d'un nombre complexe :

${\displaystyle m=|m|\left(\cos \alpha +\mathrm {i} \sin \alpha \right)}$.

En utilisant la formule d'Euler, nous en déduisons immédiatement :

Notation exponentielle d'un nombre complexe

Soit m un nombre complexe d'argument α. Nous avons alors la relation :

${\displaystyle m=|m|e^{\alpha \mathrm {i} }}$.

Cette façon d'écrire un nombre complexe est appelée « notation exponentielle d'un nombre complexe »

Formule de Moivre

Abraham de Moivre était un mathématicien. Nous pouvons très facilement retrouver sa célèbre formule en utilisant une simple propriété des puissances. On a, en effet :

${\displaystyle e^{n\alpha \mathrm {i} }=\left(e^{\alpha \mathrm {i} }\right)^{n}}$,

ce qui, en utilisant la formule d'Euler, se traduit par :

${\displaystyle \cos(n\alpha )+\mathrm {i} \sin(n\alpha )=\left(\cos \alpha +\mathrm {i} \sin \alpha \right)^{n}}$.

formule de Moivre

Soit α un angle et ${\displaystyle n}$ un entier. Cet angle vérifie la relation :

${\displaystyle \cos(n\alpha )+\mathrm {i} \sin(n\alpha )=\left(\cos \alpha +\mathrm {i} \sin \alpha \right)^{n}}$,

qui est appelée formule de Moivre.

Formules d'Euler

Si, dans la formule d'Euler, on remplace α par -α, on obtient :

${\displaystyle e^{-\alpha \mathrm {i} }=\cos(-\alpha )+\mathrm {i} \sin(-\alpha )}$

Qui, compte tenu de nos connaissances élémentaires en trigonométrie, s'écrit :

${\displaystyle e^{-\alpha \mathrm {i} }=\cos \alpha -\mathrm {i} \sin \alpha }$.

Considérons alors les deux relations :

${\displaystyle \left\{{\begin{matrix}e^{\alpha \mathrm {i} }=\cos \alpha +i\sin \alpha \\e^{-\alpha \mathrm {i} }=\cos \alpha -i\sin \alpha \end{matrix}}\right.}$

Par addition et soustraction membres à membres, nous obtenons :

${\displaystyle \left\{{\begin{matrix}e^{\alpha \mathrm {i} }+e^{-\alpha \mathrm {i} }=2\cos \alpha \\e^{\alpha \mathrm {i} }-e^{-\alpha \mathrm {i} }=2\mathrm {i} \sin \alpha \end{matrix}}\right.}$

De ces formules, nous déduisons :

Relations d'Euler

Soit α un angle. Cet angle vérifie les relations :

${\displaystyle \left\{{\begin{matrix}\cos \alpha ={\frac {e^{\alpha \mathrm {i} }+e^{-\alpha \mathrm {i} }}{2}}\\\sin \alpha ={\frac {e^{\alpha \mathrm {i} }-e^{-\alpha \mathrm {i} }}{2\mathrm {i} }},\end{matrix}}\right.}$

qui sont appelées relations d'Euler ou formules d'Euler.

cosinus ou sinus de somme d'angles

Soit ${\displaystyle a}$ et ${\displaystyle b}$ deux angles (ou deux nombres réels, cela n'a pas d'importance). Une propriété élémentaire des puissances nous permet d'écrire :

${\displaystyle e^{(a+b)i}=e^{ai}e^{bi}}$.

En utilisant la formule d'Euler pour chacune des trois exponentielles, nous obtenons :

${\displaystyle \cos(a+b)+\mathrm {i} \sin(a+b)=\left(\cos a+\mathrm {i} \sin a\right)\left(\cos b+\mathrm {i} \sin b\right)}$.

En développant le second membre, tout en tenant compte du fait que i² = -1, on obtient :

${\displaystyle \cos(a+b)+\mathrm {i} \sin(a+b)=\cos a\cos b-\sin a\sin b+\mathrm {i} \sin a\cos b+\mathrm {i} \cos a\sin b}$.

En égalant les parties réelles et imaginaires, on obtient :

Soit ${\displaystyle a}$, ${\displaystyle b}$ et ${\displaystyle c}$ trois angles (ou trois nombres réels, cela n'a toujours pas d'importance). Une propriété élémentaire des puissances nous permet d'écrire :

${\displaystyle e^{(a+b+c)\mathrm {i} }=e^{a\mathrm {i} }e^{b\mathrm {i} }e^{c\mathrm {i} }}$.

En utilisant la formule d'Euler pour chacune des quatre exponentielles, nous obtenons :

${\displaystyle \cos(a+b+c)+\mathrm {i} \sin(a+b+c)=\left(\cos a+\mathrm {i} \sin a\right)\left(\cos b+\mathrm {i} \sin b\right)\left(\cos c+\mathrm {i} \sin c\right)}$.

En développant le second membre, tout en tenant compte du fait que i² = -1, on obtient :

${\displaystyle {\begin{aligned}\cos(a+b+c)+\mathrm {i} \sin(a+b+c)&=\left(\cos a\cos b-\sin a\sin b+\mathrm {i} \sin a\cos b+\mathrm {i} \cos a\sin b\right)\left(\cos c+i\sin c\right)\\&=\cos a\cos b\cos c-\sin a\sin b\cos c+\mathrm {i} \sin a\cos b\cos c+\mathrm {i} \cos a\sin b\cos c\cdots \\&\cdots +\mathrm {i} \cos a\cos b\sin c-\mathrm {i} \sin a\sin b\sin c-\sin a\cos b\sin c-\cos a\sin b\sin c.\end{aligned}}}$

En égalant les parties réelles et imaginaires, on obtient :

Formules de dé-linéarisation

Reprenons la formule de Moivre :

Soit un nombre réel. La formule de Moivre nous donne :

${\displaystyle \cos(na)+\mathrm {i} \sin(na)=\left(\cos a+\mathrm {i} \sin a\right)^{n}}$.

Pour ${\displaystyle n=2}$, on obtient :

${\displaystyle {\begin{aligned}\cos(2a)+\mathrm {i} \sin(2a)&=\left(\cos a+\mathrm {i} \sin a\right)^{2}\\&=\cos ^{2}a+2\mathrm {i} \cos a\sin a-\sin ^{2}a\end{aligned}}}$.

En égalant les parties réelles et imaginaires, on obtient :

Pour ${\displaystyle n=3}$, on obtient :

${\displaystyle {\begin{aligned}\cos(3a)+\mathrm {i} \sin(3a)&=\left(\cos a+\mathrm {i} \sin a\right)^{3}\\&=\cos ^{3}a+3\mathrm {i} \cos ^{2}a\sin a-3\cos a\sin ^{2}a-\mathrm {i} \sin ^{3}a\end{aligned}}}$

En égalant les parties réelles et imaginaires, on obtient :

En transformant ces formules à l'aide de la formule :

${\displaystyle \cos ^{2}a+\sin ^{2}a=1}$,

on obtient d'autres formules qui peuvent être plus utiles selon les cas :

Pour ${\displaystyle n=4}$, on obtient :

${\displaystyle {\begin{aligned}\cos(4a)+\mathrm {i} \sin(4a)&=\left(\cos a+\mathrm {i} \sin a\right)^{4}\\&=\cos ^{4}a+4\mathrm {i} \cos ^{3}a\sin a-6\cos ^{2}a\sin ^{2}a-4\mathrm {i} \cos a\sin ^{3}a+\sin ^{4}a.\end{aligned}}}$

En égalant les parties réelles et imaginaires, on obtient :

En transformant ces formules à l'aide de la formule :

${\displaystyle \cos ^{2}a+\sin ^{2}a=1}$,

on obtient d'autres formules qui peuvent être plus utiles selon les cas :

etc. (on verra au niveau 14 un exercice qui systématise ces calculs).

Formules de linéarisation

Ce sont des formules trigonométriques qui permettent de faire disparaître les produits et les puissances dans des expressions trigonométriques. Elles sont nombreuses et utiles. Nous allons voir les plus simples, mais le principe reste le même pour les formules plus compliquées.

Elles utilisent les formules d'Euler

${\displaystyle {\begin{aligned}\cos ^{2}\alpha &=\left({\frac {e^{\alpha \mathrm {i} }+e^{-\alpha \mathrm {i} }}{2}}\right)^{2}={\frac {\left(e^{\alpha \mathrm {i} }+e^{-\alpha \mathrm {i} }\right)^{2}}{4}}\\&={\frac {\left(e^{\alpha \mathrm {i} }\right)^{2}+2e^{\alpha \mathrm {i} }e^{-\alpha \mathrm {i} }+\left(e^{-\alpha \mathrm {i} }\right)^{2}}{4}}\\&={\frac {e^{2\alpha \mathrm {i} }+2e^{\alpha \mathrm {i} -\alpha \mathrm {i} }+e^{-2\alpha \mathrm {i} }}{4}}\\&={\frac {e^{2\alpha \mathrm {i} }+e^{-2\alpha \mathrm {i} }+2e^{0}}{4}}\\&={\frac {2\cos(2\alpha )+2}{4}}\\&={\frac {\cos(2\alpha )+1}{2}}\end{aligned}}}$

Nous avons bien détaillé le calcul pour que vous compreniez bien. Nous le détaillerons moins par la suite.

Nous avons obtenu :

${\displaystyle {\begin{aligned}\sin ^{2}\alpha &=\left({\frac {e^{\alpha \mathrm {i} }-e^{-\alpha \mathrm {i} }}{2\mathrm {i} }}\right)^{2}={\frac {\left(e^{\alpha \mathrm {i} }-e^{-\alpha \mathrm {i} }\right)^{2}}{-4}}\\&={\frac {\left(e^{\alpha \mathrm {i} }\right)^{2}-2e^{\alpha \mathrm {i} }e^{-\alpha \mathrm {i} }+\left(e^{-\alpha \mathrm {i} }\right)^{2}}{-4}}\\&={\frac {e^{2\alpha \mathrm {i} }-2e^{\alpha \mathrm {i} -\alpha \mathrm {i} }+e^{-2\alpha \mathrm {i} }}{-4}}\\&={\frac {e^{2\alpha \mathrm {i} }+e^{-2\alpha \mathrm {i} }-2e^{0}}{-4}}\\&={\frac {2\cos(2\alpha )-2}{-4}}\\&={\frac {1-\cos(2\alpha )}{2}}\end{aligned}}}$

Nous avons obtenu :

${\displaystyle {\begin{aligned}\cos ^{3}\alpha &=\left({\frac {e^{\alpha \mathrm {i} }+e^{-\alpha \mathrm {i} }}{2}}\right)^{3}={\frac {\left(e^{\alpha \mathrm {i} }+e^{-\alpha \mathrm {i} }\right)^{3}}{8}}\\&={\frac {\left(e^{\alpha \mathrm {i} }\right)^{3}+3e^{2\alpha \mathrm {i} }e^{-\alpha \mathrm {i} }+3e^{\alpha \mathrm {i} }e^{-2\alpha \mathrm {i} }+\left(e^{-\alpha \mathrm {i} }\right)^{3}}{8}}\\&={\frac {e^{3\alpha \mathrm {i} }+3e^{2\alpha \mathrm {i} -\alpha \mathrm {i} }+3e^{\alpha \mathrm {i} -2\alpha \mathrm {i} }+e^{-3\alpha \mathrm {i} }}{8}}\\&={\frac {\left(e^{3\alpha \mathrm {i} }+e^{-3\alpha \mathrm {i} }\right)+3\left(e^{\alpha \mathrm {i} }+e^{-\alpha \mathrm {i} }\right)}{8}}\\&={\frac {2\cos(3\alpha )+6\cos \alpha }{8}}\\&={\frac {\cos(3\alpha )+3\cos \alpha }{4}}\end{aligned}}}$

Nous avons obtenu :

${\displaystyle {\begin{aligned}\cos ^{2}\alpha \sin \alpha &=\left({\frac {e^{\alpha \mathrm {i} }+e^{-\alpha \mathrm {i} }}{2}}\right)^{2}\left({\frac {e^{\alpha \mathrm {i} }-e^{-\alpha \mathrm {i} }}{2\mathrm {i} }}\right)\\&={\frac {\left(e^{2\alpha \mathrm {i} }+2+e^{-2\alpha \mathrm {i} }\right)\left(e^{\alpha \mathrm {i} }-e^{-\alpha \mathrm {i} }\right)}{8\mathrm {i} }}\\&={\frac {e^{3\alpha \mathrm {i} }-e^{\alpha \mathrm {i} }+2e^{\alpha \mathrm {i} }-2e^{-\alpha \mathrm {i} }+e^{-\alpha \mathrm {i} }-e^{-3\alpha \mathrm {i} }}{8\mathrm {i} }}\\&={\frac {e^{3\alpha \mathrm {i} }-e^{-3\alpha \mathrm {i} }+e^{\alpha \mathrm {i} }-e^{-\alpha \mathrm {i} }}{8\mathrm {i} }}\\&={\frac {2\mathrm {i} \sin(3\alpha )+2\mathrm {i} \sin \alpha }{8\mathrm {i} }}\\&={\frac {\sin(3\alpha )+\sin \alpha }{4}}\end{aligned}}}$

Nous avons obtenu :

${\displaystyle {\begin{aligned}\cos \alpha \sin ^{2}\alpha &=\left({\frac {e^{\alpha \mathrm {i} }+e^{-\alpha \mathrm {i} }}{2}}\right)\left({\frac {e^{\alpha \mathrm {i} }-e^{-\alpha \mathrm {i} }}{2\mathrm {i} }}\right)^{2}\\&={\frac {\left(e^{\alpha \mathrm {i} }+e^{-\alpha \mathrm {i} }\right)\left(e^{2\alpha \mathrm {i} }-2+e^{-2\alpha \mathrm {i} }\right)}{-8}}\\&={\frac {e^{3\alpha \mathrm {i} }+e^{\alpha \mathrm {i} }-2e^{\alpha \mathrm {i} }-2e^{-\alpha \mathrm {i} }+e^{-\alpha \mathrm {i} }+e^{-3\alpha \mathrm {i} }}{-8}}\\&={\frac {e^{3\alpha \mathrm {i} }+e^{-3\alpha \mathrm {i} }-e^{\alpha \mathrm {i} }-e^{-\alpha \mathrm {i} }}{-8}}\\&={\frac {2\cos(3\alpha )-2\cos \alpha }{-8}}\\&={\frac {-\cos(3\alpha )+\cos \alpha }{4}}\end{aligned}}}$

Nous avons obtenu :

${\displaystyle {\begin{aligned}\sin ^{3}\alpha &=\left({\frac {e^{\alpha \mathrm {i} }-e^{-\alpha \mathrm {i} }}{2\mathrm {i} }}\right)^{3}={\frac {\left(e^{\alpha \mathrm {i} }-e^{-\alpha \mathrm {i} }\right)^{3}}{-8\mathrm {i} }}\\&={\frac {e^{3\alpha i}-e^{-3\alpha i}-3e^{\alpha i}+3e^{-\alpha i}}{-8i}}\\&={\frac {2\mathrm {i} \sin(3\alpha )-6\mathrm {i} \sin \alpha }{-8\mathrm {i} }}\\&={\frac {-\sin(3\alpha )+3\sin \alpha }{4}}\end{aligned}}}$

Nous avons obtenu :

${\displaystyle {\begin{aligned}\cos ^{4}\alpha &=\left({\frac {e^{\alpha \mathrm {i} }+e^{-\alpha \mathrm {i} }}{2}}\right)^{4}={\frac {\left(e^{\alpha \mathrm {i} }+e^{-\alpha \mathrm {i} }\right)^{4}}{16}}\\&={\frac {e^{4\alpha \mathrm {i} }+4e^{2\alpha \mathrm {i} }+6+4e^{-2\alpha \mathrm {i} }+e^{-4\alpha \mathrm {i} }}{16}}\\&={\frac {\left(e^{4\alpha \mathrm {i} }+e^{-4\alpha \mathrm {i} }\right)+4\left(e^{2\alpha \mathrm {i} }+e^{-2\alpha \mathrm {i} }\right)+6}{16}}\\&={\frac {2\cos(4\alpha )+8\cos(2\alpha )+6}{16}}\\&={\frac {\cos(4\alpha )+4\cos(2\alpha )+3}{8}}\end{aligned}}}$

Nous avons obtenu :

etc.

Somme de cosinus et de sinus

Nous avons :

${\displaystyle {\begin{aligned}e^{a\mathrm {i} }+e^{b\mathrm {i} }&=e^{i{\frac {a+b}{2}}}\left(e^{\mathrm {i} {\frac {a-b}{2}}}+e^{-\mathrm {i} {\frac {a-b}{2}}}\right)\\&=2e^{\mathrm {i} {\frac {a+b}{2}}}\cos \left({\frac {a-b}{2}}\right)\end{aligned}}}$

En utilisant la formule d'Euler, on obtient alors :

${\displaystyle \cos a+\mathrm {i} \sin a+\cos b+\mathrm {i} \sin b=2\left(\cos {\frac {a+b}{2}}+\mathrm {i} \sin {\frac {a+b}{2}}\right)\cos {\frac {a-b}{2}}}$.

En identifiant les parties réelles et les parties imaginaires, on obtient finalement :

Nous avons aussi :

${\displaystyle {\begin{aligned}e^{a\mathrm {i} }-e^{b\mathrm {i} }&=e^{\mathrm {i} {\frac {a+b}{2}}}\left(e^{\mathrm {i} {\frac {a-b}{2}}}-e^{-\mathrm {i} {\frac {a-b}{2}}}\right)\\&=2\mathrm {i} e^{\mathrm {i} {\frac {a+b}{2}}}\sin \left({\frac {a-b}{2}}\right)\end{aligned}}}$

En utilisant la formule d'Euler, on obtient alors :

${\displaystyle \cos a+\mathrm {i} \sin a-\cos b-\mathrm {i} \sin b=2\mathrm {i} \left(\cos {\frac {a+b}{2}}+\mathrm {i} \sin {\frac {a+b}{2}}\right)\sin {\frac {a-b}{2}}}$.

En identifiant les parties réelles et les parties imaginaires, on obtient finalement :

Produit de cosinus et de sinus

Nous avons :

${\displaystyle {\begin{aligned}\cos a\cos b&=\left({\frac {e^{\mathrm {i} a}+e^{-\mathrm {i} a}}{2}}\right)\left({\frac {e^{\mathrm {i} b}+e^{-\mathrm {i} b}}{2}}\right)\\&={\frac {e^{\mathrm {i} (a+b)}+e^{\mathrm {i} (a-b)}+e^{-\mathrm {i} (a-b)}+e^{-\mathrm {i} (a+b)}}{4}}\\&={\frac {2\cos(a+b)+2\cos(a-b)}{4}}\end{aligned}}}$

Nous avons obtenu :

Nous avons aussi :

${\displaystyle {\begin{aligned}\sin a\sin b&=\left({\frac {e^{\mathrm {i} a}-e^{-\mathrm {i} a}}{2\mathrm {i} }}\right)\left({\frac {e^{\mathrm {i} b}-e^{-\mathrm {i} b}}{2\mathrm {i} }}\right)\\&={\frac {e^{\mathrm {i} (a+b)}-e^{\mathrm {i} (a-b)}-e^{-\mathrm {i} (a-b)}+e^{-\mathrm {i} (a+b)}}{-4}}\\&={\frac {2\cos(a+b)-2\cos(a-b)}{-4}}\end{aligned}}}$

Nous avons obtenu :

Nous avons enfin :

${\displaystyle {\begin{aligned}\sin a\cos b&=\left({\frac {e^{\mathrm {i} a}-e^{-\mathrm {i} a}}{2i}}\right)\left({\frac {e^{\mathrm {i} b}+e^{-\mathrm {i} b}}{2}}\right)\\&={\frac {e^{\mathrm {i} (a+b)}+e^{\mathrm {i} (a-b)}-e^{-\mathrm {i} (a-b)}-e^{-\mathrm {i} (a+b)}}{4\mathrm {i} }}\\&={\frac {2\mathrm {i} \sin(a+b)+2\mathrm {i} \sin(a-b)}{4\mathrm {i} }}\end{aligned}}}$

Nous avons obtenu :