Exercice 8-1
Déterminez le réel a pour que la fonction f définie ci-dessous soit dérivable pour x0 = 0. Étudiez alors la fonction f :
f sera dérivable pour x = 0 si sa dérivée à gauche en 0 est égale à sa dérivée en droite en 0, c'est-à-dire si :
qui s'écrit :
soit :
La dérivée de f est alors définie par :
Nous voyons que la dérivée s'annule pour x = -5/2 et x = 5/2. Une étude du signe de la dérivée sur chaque intervalle nous donne le tableau de variation suivant :
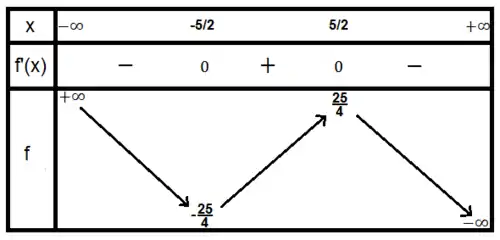
Nous obtenons la courbe représentative suivante :
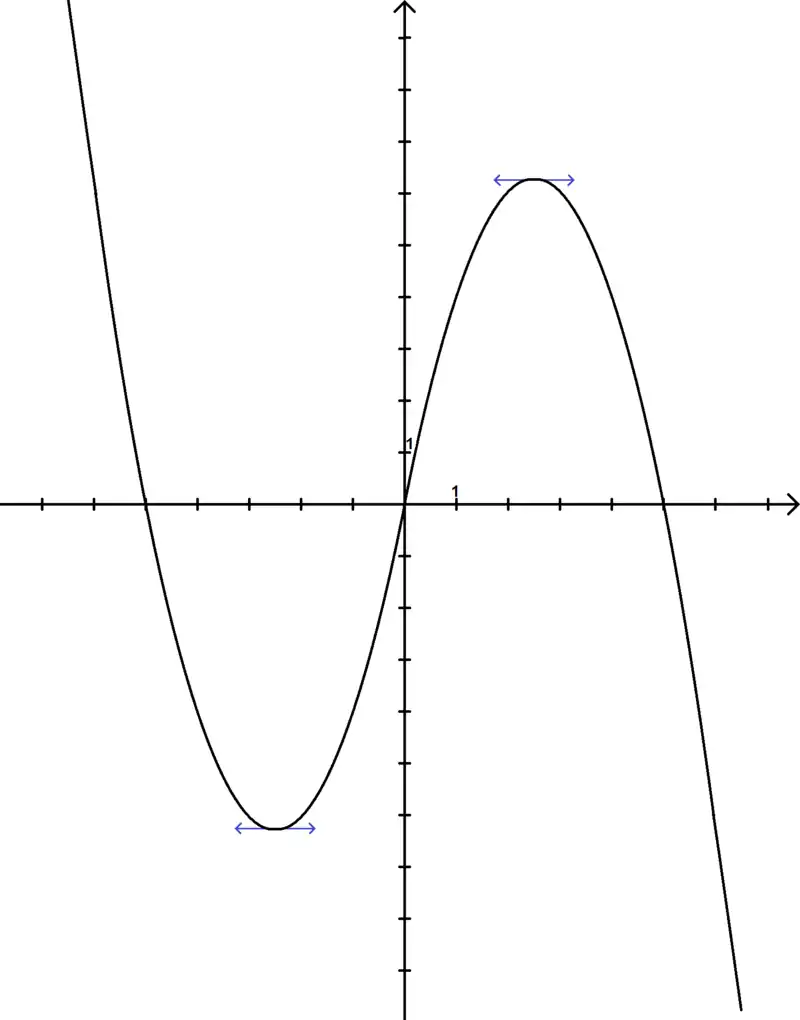
Exercice 8-2
1° Déterminer les réels a, b, c pour que la fonction f, définie par :
- présente un minimum égal à pour x = et pour qu'elle prenne la valeur 1 pour x = 1.
2° Représenter graphiquement la fonction f obtenue précédemment.
3° Discuter, en fonction de m, le nombre de points d'intersection de la courbe C obtenue au 2° et de la droite D d'équation y = mx.
4° Si D coupe C en deux points M' et M", on considère le milieu I de [M'M"]. Quel est l'ensemble décrit par I lorsque m varie ?
1° La dérivée de f est :
Si la fonction f présente un minimum pour x = , cela signifie que la dérivée s'annule pour cette valeur, on a donc :
Si le minimum pour x = est égal à , on a aussi :
De plus, on sait que pour x = 1, la fonction vaut 1, on a donc :
En simplifiant et en réunissant les trois relations précédentes en un système de trois équations à trois inconnues, on obtient :
La résolution de ce système est :
La fonction f sera donc définie par :
2°
Le tracé de la courbe f est une parabole.
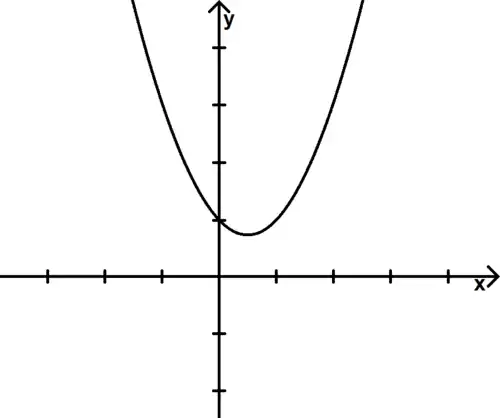
3°
Le tracé de f (parabole) interceptera le tracée de la droite d'équation y = mx lorsque :
que l'on peut écrire :
Il nous suffit donc d'étudier le nombre de racines réelles de cette équation et cela dépend du signe du discriminant qui est égal à :
En résolvant l'équation :
On voit que le discriminant est nul pour m = -3 et m = 1.
On aura donc :
- pour m = -3 ou m = 1, le discriminant est nul, ce qui entraîne qu'il y a une seule interception entre la parabole et la droite (On pourrait montrer que la droite est tangente à la parabole).
- Pour m strictement compris entre -3 et 1, le discriminant sera strictement négatif et donc il n'y aura aucun point d'interception entre la parabole et la droite.
- Pour m strictement non compris entre -3 et 1, le discriminant sera strictement positif et il y aura donc deux points d'interception entre la parabole et la droite.
4°
Si la droite et la parabole se coupent en deux points distincts M' et M", cela signifie que le discriminant de l'équation :
est strictement positif. Et, par conséquent, m est strictement non compris entre -3 et 1.
L'équation :
a donc deux racines x1 et x2 (respectivement abscisses des points M' et M"). Le milieu I des points d'interception entre la courbe et la parabole aura donc pour abscisse :
(On rappelle que la somme des racines de l'équation ax2 + bx + c = 0 est donnée par -b/a)
L'ordonnée de I sera :
Le point I a donc pour coordonnées :
Soit x et y, l'abscisse et l'ordonnée de I, on aura :
Pour mieux se rendre compte de quel type de courbe parcourt I lorsque m varie de à -3 et de 1 à , il nous faut éliminer m entre l'expression de x et de y. De la première équation, nous tirons :
et en portant dans la deuxième équation, nous obtenons :
Nous voyons que I parcourt un morceau de parabole d'équation y = 2x2-x.
Exercice 8-3
Déterminer les réels a, b, c et d pour que la courbe représentative de la fonction f définie par :
contienne les points A(0,2), B(1,4), C(2,-2) et D(3,0).
Étudier ensuite cette fonction.
Les coordonnées des points A, B, C, D doivent vérifier :
De la première équation, nous tirons b = 2d que nous pouvons porter dans les autres équations :
De la quatrième équation, nous tirons a = -2d/3 que nous pouvons porter dans les autres équations :
En simplifiant les deux dernières équations, on trouve :
Nous remarquons que les deux dernières équations sont identiques, ce qui produit une indétermination. Exprimons donc a, b, c en fonction de d :
Et nous voyons que l'on peut obtenir un système simple de solution en choisissant d = -3, on obtient :
La fonction f recherchée est donc défini par :
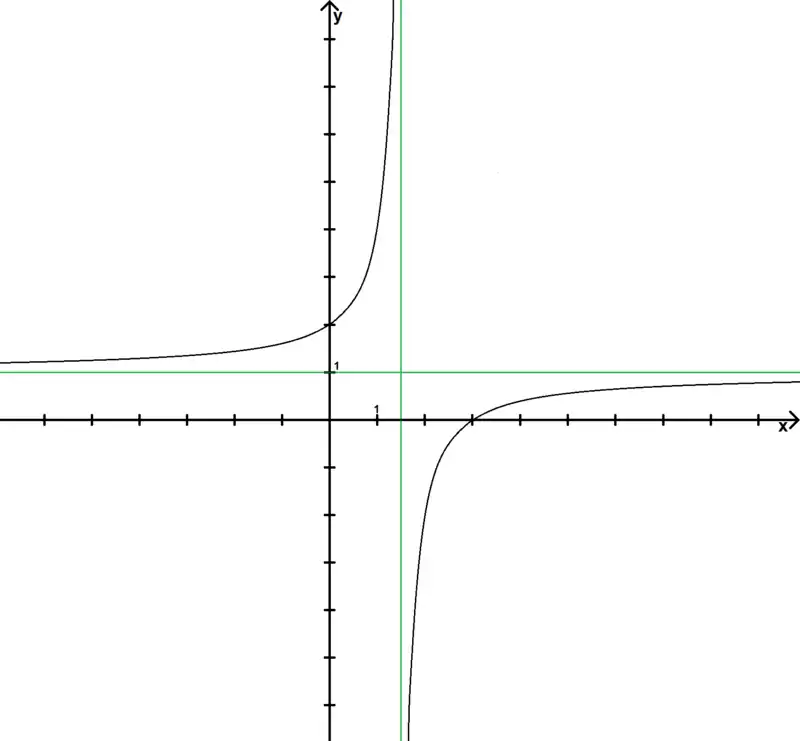
Nous reconnaissons une hyperbole de domaine de définition :
L'étude des limites aux bornes du domaine de définition nous donne :
Nous en déduisons le tableau de variation suivant :
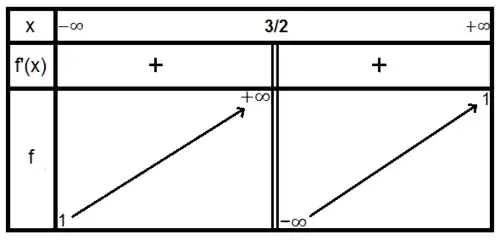
Ou l'on voit une asymptote horizontale d'équation et une asymptote verticale d'équation
Nous obtenons alors la courbe représentative de f suivante :
Exercice 8-4
1° Dans un repère orthonormé, construire la courbe H représentative de la fonction f définie par :
- Soit I son centre de symétrie.
2° Déterminer le coefficient directeur de la tangente à H au point A d'abscisse 2. Quel est l'autre tangente à H ayant le même coefficient directeur. Soit A', le point de contact de cette dernière. Étudier la position relative des points A, I et A'.
3° Quelles sont les valeurs du réel m pour lesquelles la droite D d'équation y = -2x + m rencontre la courbe H en deux points M et M' (distincts ou confondus)?
4° Lorsque m satisfait à la condition trouvée, calculer, en fonction de m, les coordonnées du milieu J de [MM']. Préciser l'ensemble décrit par J quand m varie.
1°
La courbe représentative H de f est une hyperbole de domaine de définition :
L'étude des limites aux bornes du domaine de définition nous permet d'établir le tableau de variation suivant :
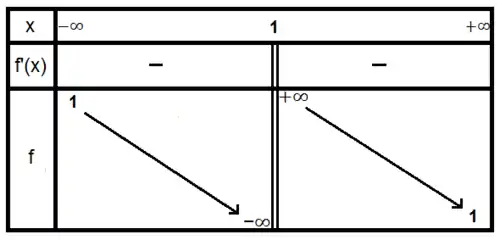
Où l'on voit une asymptote horizontale d'équation y = 1 et une asymptote verticale d'équation x = 1
Nous en déduisons la courbe représentative de f suivante :
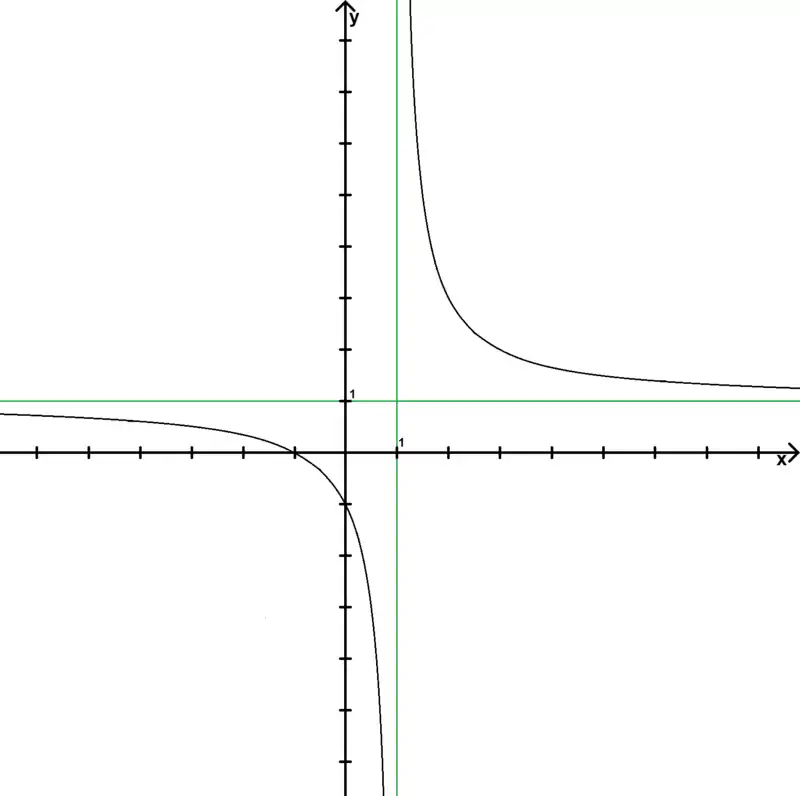
Le centre de symétrie d'une hyperbole est le point d'interception de ses asymptotes. I aura donc pour abscisse 1 et pour ordonnée 1.
2°
Le coefficient directeur de la tangente en A à la courbe est donné par le nombre dérivée en A. Calculons donc la dérivée de f :
Le coefficient directeur de la tangente en A sera donc :
Recherchons une autre tangente à la courbe H ayant même coefficient directeur (donc parallèle à la première tangente). Pour cela, il nous faut résoudre l'équation :
C'est-à-dire :
équivalente sur Df à :
On trouve x = 2 ou x = 0.
On sait que 2 est l'abscisse de A, donc l'abscisse de A' sera 0. L'ordonnée de A' sera f(0) = -1.
I a pour coordonnées (1;1), A a pour coordonnées (2; 3), A' a pour coordonnées (0; -1). Nous voyons que I est le milieu du segment [AA']
3°
Pour trouver les abscisses des points d'interception entre l'hyperbole H et la droite D, il nous faut résoudre l'équation :
qui s'écrit aussi :
On obtient une équation du second degré. Par conséquent, il y aura deux points d'interceptions (distincts ou confondus) si le discriminant de l'équation est positif ou nul. C'est-à-dire si :
En factorisant, on obtient :
C'est-à-dire si m appartient à l'intervalle :
4°
Si m appartient à l'intervalle :
l'équation :
a donc deux racines x1 et x2 (respectivement abscisses des points M et M'). Le milieu J des points d'interception entre la droite D et l'hyperbole H aura donc pour abscisse :
(On rappelle que la somme des racines de l'équation ax2 + bx + c = 0 est donnée par -b/a)
L'ordonnée de J sera :
Le point J a donc pour coordonnées :
Soit x et y, l'abscisse et l'ordonnée de I, on aura :
Pour mieux se rendre compte sur quel type de courbe se trouve J lorsque H et D se coupent , il nous faut éliminer m entre l'expression de x et de y. De la première équation, nous tirons :
et en portant dans la deuxième équation, nous obtenons :
Nous voyons que J parcourt une partie de la droite d'équation y = 2x - 1.
Exercice 8-5
1° Étudier la fonction f définie par :
2° Une droite D parallèle à la droite des abscisses coupe la courbe, en général, en deux points M' et M" qui se projette en P' et P" sur cette droite des abscisses. Démontrer qu'il existe un point A de x'Ox tel que :
- soit constant.
1°
Domaine de définition
Le dénominateur :
ne doit pas être nul. Par conséquent :
Limites aux bornes du domaine de définition
Calcul de la dérivée
Tableau de variations
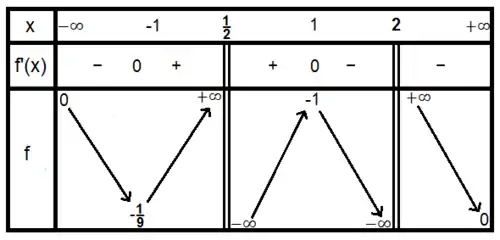
Études des asymptotes
Nous indique que nous avons une asymptote horizontale d'équation
Nous indique que nous avons une asymptote verticale d'équation
Nous indique que nous avons une asymptote verticale d'équation
Tracé de la courbe
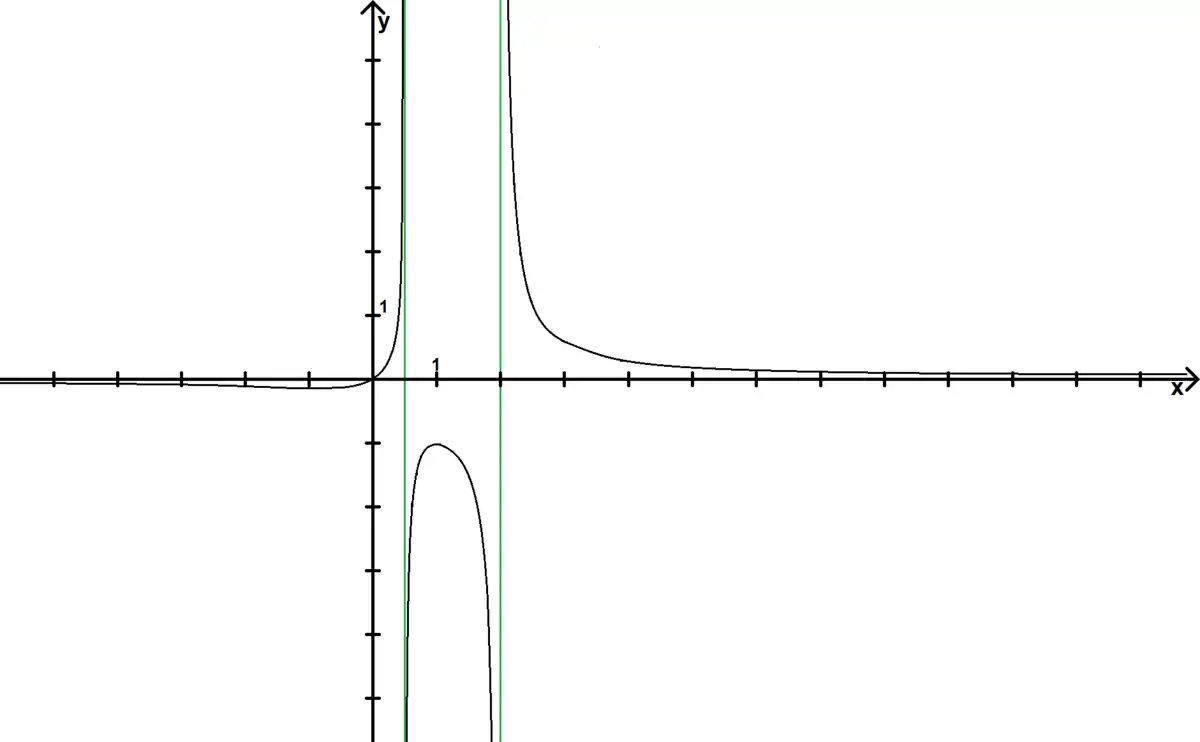
2°
Une droite parallèle à l'axe des abscisses a pour équation y = m (m étant un paramètre). Les abscisses de M' et M" sont donc les solutions de l'équation :
qui s'écrit après transformation :
Qui est du second degré et qui a bien deux racines lorsque son discriminant est positif. Soit donc x1 et x2 les deux racines qui sont donc les abscisses de M' et M", mais aussi les abscisses de P' et P".
Soit aussi a l'abscisse du point A. On a alors :
La première fraction ne contient plus m. Si l'on veut rendre l'expression obtenue indépendante de m, il suffit de choisir une valeur de a qui annule la deuxième fraction qui contient encore m. Nous voyons qu'il suffit de choisir a = 0, c'est-à-dire A à l'origine du repère, et il nous reste :
qui est indépendant de m et donc indépendamment de la droite D choisi.
Exercice 8-6
1° Étudier la fonction f définie par :
2° À tout réel λ, on peut associer en général deux réels x' et x" dont les images par f sont égales à λ.
- Calculer x' + x" et x'x" en fonction de λ. En déduire une relation indépendante de λ liant x' et x".
3° Comment faut-il choisir λ pour que x' et x" soient égaux ? interpréter graphiquement ce cas.
1°
Domaine de définition
Le dénominateur :
ne peut pas être nul. Par conséquent :
Limites aux bornes du domaine de définition
Calcul de la dérivée
Les valeurs qui annulent la dérivée sont donc les racines de l'équation :
on trouve :
Le maximum est :
Par un calcul très similaire, on trouve que le minimum est :
Tableau de variations
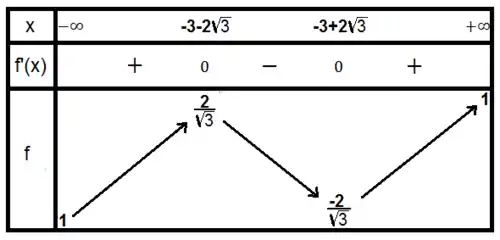
Études des asymptotes
Nous indique que nous avons une asymptote horizontale d'équation
Étudions la position de la courbe par rapport à l'asymptote horizontale :
Nous voyons que f(x) - y est positif pour x < -3 et négatif pour x > 3. Ce qui signifie que pour les valeurs de x inférieure à -3, la courbe est en dessus de l'asymptote et pour les valeurs de x supérieure à 3 la courbe est en dessous de l'asymptote. Et, bien sûr, la courbe coupe l'asymptote pour x = 3.
Tracé de la courbe
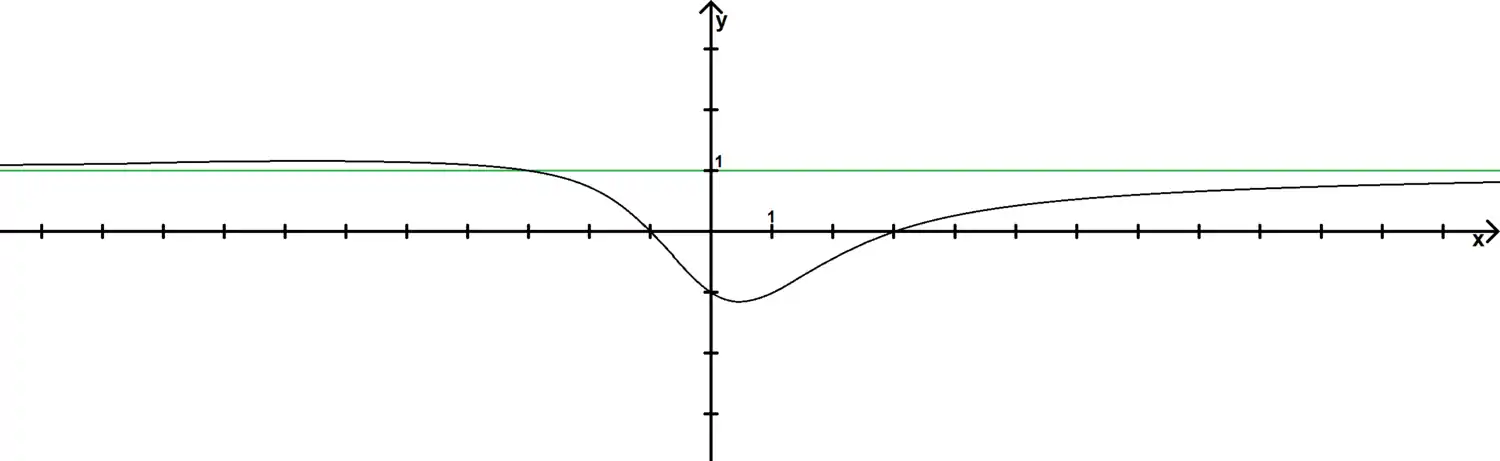
2°
x' et x" sont les racines de l'équation :
qui, après transformation, s'écrit :
On rappelle que pour une équation ax2 + bx + c = 0, la somme des racines est -b/a et le produit des racines est c/a. Par conséquent on a :
Pour trouver une relation entre x' et x" indépendante de λ, il nous suffit d'éliminer λ entre les deux relations ci-dessus. De la première relation, on tire :
En portant dans la deuxième relation, on obtient :
qui se simplifie en :
3°
Supposons x' et x" égaux et posons :
Alors :
devient :
Éliminons cette fois r entre ces deux relations. Nous obtenons :
qui donne après simplification :
Soit :
Nous voyons que l'on obtient pour λ deux valeurs possibles : une des valeurs correspond à la valeur du minimum de la courbe et l'autre valeur correspond à la valeur du maximum de la courbe.