Approche
- Soit .
Que se passe-t-il lorsque devient de plus en plus grand, autrement dit, lorsque tend vers l'infini ?
tend également vers l'infini.
On note : .
On énonce : « la limite de quand tend vers est égale à ».
De même, nous pouvons écrire : .
Intéressons-nous maintenant à une valeur précise de . Par exemple, pour , . Mais alors si tend vers 4, va s'approcher de plus en plus de : .
- Soit .
Si est un réel quelconque, on a bien : .
Lorsque devient très grand, nous pouvons concevoir que devient très petit, se rapprochant de 0 : .
De même, quand prend des valeurs négatives dont la valeur absolue est très grande, .
- Soit . Essayons de calculer sa limite aux infinis :
- or nous savons que :
- donc et finalement .
- Plus généralement, calculons la limite d'une fonction polynôme :
- Soit .
- .
- Or :
- lorsque
- d'où :
- et : .
Nous retiendrons qu'une fonction polynôme se comporte, aux infinis, comme son terme de plus haut degré.
Définition
Limite finie en l'infini
- Soit une fonction définie d'un nombre réel jusqu'à l'infini. Soit un nombre réel. On dit que tend vers quand tend vers si et seulement si tout intervalle ouvert contenant contient aussi toutes les valeurs de pour assez grand. On écrit :
- On dit que tend vers quand tend vers si et seulement si tout intervalle ouvert contenant contient aussi toutes les valeurs de pour assez grand (ou assez petit, pouvant être négatif). On écrit :
Interprétation graphique
admet une asymptote horizontale d'équation au voisinage de
L'asymptote d'une courbe représentative d'une fonction dans un plan est une droite qui partage une limite commune avec la fonction étudiée. L'équation de cette asymptote dépend de la situation de la limite commune (en l'infini ou en un point...)
Limite infinie en l'infini
- On dit que la fonction tend vers quand tend vers si et seulement si tout intervalle avec un nombre réel contient toutes les valeurs de pour suffisamment grand. On écrit :
- On dit que la fonction tend vers quand tend vers si et seulement si tout intervalle avec un nombre réel contient toutes les valeurs de pour suffisamment grand. On écrit :
- On écrit :
ou
si et seulement si tout intervalle avec un nombre réel contient toutes les valeurs de pour suffisamment petit.
- On écrit :
ou
si et seulement si tout intervalle avec un nombre réel contient toutes les valeurs de pour suffisamment petit.
Limite finie ou infinie en un réel
- Soit une fonction définie sur un intervalle ouvert contenant un nombre réel .
On dit que tend vers quand tend vers si et seulement si tout intervalle ouvert contenant contient aussi toutes les valeurs de pour tout réel de assez proche de . On écrit :
- On dit que tend vers quand tend vers si et seulement si tout intervalle avec un nombre réel contient toutes les valeurs de pour suffisamment proche de . On écrit :
- On dit que tend vers quand tend vers si et seulement si tout intervalle avec un nombre réel contient toutes les valeurs de pour suffisamment proche de . On écrit :
Interprétation graphique
Si (ou ) alors admet une asymptote verticale d'équation au voisinage de .
Limite aux infinis de fonctions de référence
Exemple 1
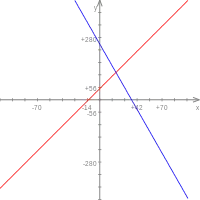
| Si | Si |
Exemple 2
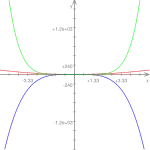
Exemple 3
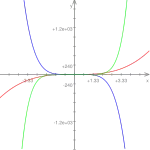
Exemple 4
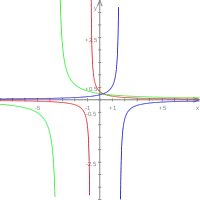
avec
Exemple 5
D'autres outils pour les limites
Théorèmes
Théorème de comparaison
Soit et deux fonctions définies sur un intervalle du type (ou ) avec un nombre réel telles que pour tout appartenant à cette intervalle, .
Si alors
Théorème de l'encadrement (dit "théorème des gendarmes")
Soit , et trois fonctions définies sur un intervalle du type (ou ) avec un nombre réel telles que pour tout appartenant à cette intervalle, .
Si avec un nombre réel ou ou alors
Asymptotes
La courbe représentative de la fonction inverse, lorsque est de plus en plus grand ou de plus en plus petit, se rapproche de l’axe des abscisses mais sans la toucher. Cette dernière est en fait une asymptote horizontale de la fonction inverse.
De même, la courbe se rapproche également de l’axe des ordonnées, sans jamais la croiser, lorsque tend vers 0. Nous avons là une asymptote verticale de la fonction.
Asymptote horizontale et verticale
Dire que la courbe représentative d'une fonction se rapproche d'une droite horizontale d'équation quand devient très grand (ou très petit) signifie que tend vers la valeur quand tend vers l'infini.
Ainsi, la droite est asymptote horizontale de si et seulement si .
Quand la courbe représentative de rapproche d'une droite verticale d'équation , c’est qui tend vers l'infini cette fois, lorsque x se rapproche de cette valeur .
On a :
Chercher une asymptote horizontale d'une fonction revient à calculer la limite en de cette fonction.
Lorsqu’il y a une asymptote verticale en , la courbe de la fonction ne touche pas la droite, et donc n’est pas définie ; il s'agit d'une borne du domaine de définition de la fonction.
Chercher une asymptote verticale d'une fonction revient alors à calculer les limites aux bornes du domaine de définition de cette fonction.
Asymptote oblique
Soit une fonction définie sur un intervalle (ou ) avec un nombre réel telle que l’on ait :
.
Alors la droite d'équation est une asymptote oblique à la courbe représentative de au voisinage de (ou ).
Limite de la composée de deux fonctions
Les lettres , et désignent soit des nombres réels, soit soit .
Soit la fonction composée définie sur un intervalle contenant , ou dont est une borne.
Si et si alors