Théorème de Pascal

Il y a équivalence entre les deux propositions suivantes concernant un hexagone d'un plan projectif

• (i) l'hexagone est inscrit dans une conique ;
• (ii) les intersections des 3 paires de côtés opposés sont alignées.

Si deux côtés opposés sont confondus, leur intersection n'est évidemment pas unique. Le théorème s'interprète alors par exemple en écrivant la seconde condition sous la forme : « Il existe une droite contenant trois points appartenant aux intersections respectives des paires de côtés opposés ». Cependant cette disposition ne peut exister dans le cas d'une conique propre puisque l'intersection d'une telle conique et d'une droite comporte au plus deux points.

Le théorème de Pappus est un cas particulier du théorème (direct) de Pascal, lorsque la conique est dégénérée en deux droites distinctes D et D'. De plus, pour obtenir un résultat non trivial (vérification immédiate), on suppose que les deux sommets de chaque côté appartiennent à des droites D, D' distinctes.

On peut remarquer en reprenant la démonstration dans ce cas que les résultats généraux d'homographie sur une conique ne sont pas réellement utilisés. Les théorèmes invoqués sont plus simplement ceux concernant les divisions de points alignés et les faisceaux de droites.

Théorème de Pascal

Étant donné un hexagone inscrit dans un cercle, les intersections des côtés opposés sont alignées.

On veut prouver l'alignement de ${\displaystyle M,N,P}$ ; on utilisera donc le théorème de Ménélaüs. Un triangle envisageable pour ce théorème est obtenu avec les droites ${\displaystyle (BC),(DE),(FA)}$ qui donnent les points ${\displaystyle I,J,K}$ (un autre celui construit avec ${\displaystyle (AB),(CD),(EF)}$). Les côtés non utilisés de l'hexagone fournissent des points alignés avec ${\displaystyle M,N,P}$, d'où des utilisations possibles de Menelaüs qui traduisent en fait la façon dont la figure est construite. Il suffit alors d'utiliser le fait que tous ces points sont sur un même cercle, ce qui justifie l'utilisation de la puissance d'un point.

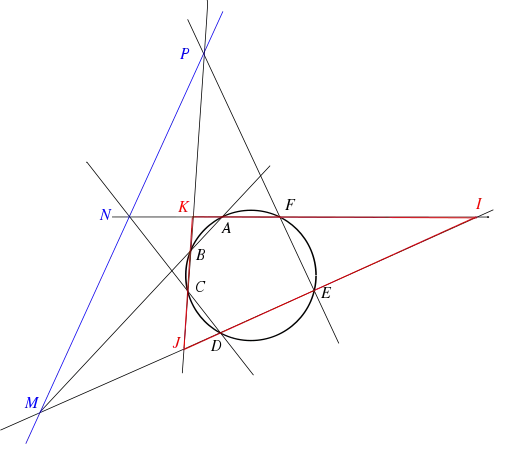
On veut donc calculer ${\displaystyle \prod ={\frac {\overline {MI}}{\overline {MJ}}}\,{\frac {\overline {PJ}}{\overline {PK}}}\,{\frac {\overline {NK}}{\overline {NI}}}}$.

En utilisant le théorème de Ménélaüs dans le triangle ${\displaystyle IJK}$ et le fait que ${\displaystyle M,A,B}$ soient alignés, on tire ${\displaystyle {\frac {\overline {MI}}{\overline {MJ}}}\,{\frac {\overline {BJ}}{\overline {BK}}}\,{\frac {\overline {AK}}{\overline {AI}}}=1}$

d'où ${\displaystyle {\frac {\overline {MI}}{\overline {MJ}}}={\frac {\overline {BK}}{\overline {BJ}}}\,{\frac {\overline {AI}}{\overline {AK}}}.}$ On a également des relations similaires en écrivant que ${\displaystyle N,D,C}$ et ${\displaystyle P,E,F}$ sont alignés. Tout ceci donne ${\displaystyle \prod ={\Big (}{\frac {\overline {BK}}{\overline {BJ}}}\,{\frac {\overline {AI}}{\overline {AK}}}{\Big )}{\Big (}{\frac {\overline {EJ}}{\overline {EI}}}\,{\frac {\overline {FI}}{\overline {FK}}}{\Big )}{\Big (}{\frac {\overline {CK}}{\overline {CJ}}}\,{\frac {\overline {DJ}}{\overline {DI}}}{\Big )}.}$

En utilisant la puissance de ${\displaystyle I,J,K}$ par rapport au cercle, on tire ${\displaystyle {\overline {BK}}\,{\overline {CK}}={\overline {AK}}\,{\overline {FK}}}$, ${\displaystyle {\overline {AI}}\,{\overline {FI}}={\overline {EI}}\,{\overline {DI}}}$ et finalement ${\displaystyle {\overline {EJ}}\,{\overline {DJ}}={\overline {BJ}}\,{\overline {CJ}}}$ si bien que ${\displaystyle \prod =1}$.

La droite que forme cet alignement est appelée « droite de Pascal ». La figure obtenue par la construction est appelée « hexagramme de Pascal ».

Nota bene : tout dépend du système d'axiomes choisis, mais les points d'intersection de deux droites existent toujours si on adopte les axiomes de la géométrie projective qui ignore le parallélisme.

En prenant la polaire de cet énoncé par rapport au cercle lui-même, nous obtenons l'énoncé dit « dual » du précédent

Théorème de Brianchon

Étant donné un hexagone circonscrit à un cercle, les diagonales sont concourantes.

Ci-dessous le dessin dual du précédent. Les points ont été remplacés par les tangentes correspondantes ; le point de concours est le pôle de la droite précédente, ce qui est mis en évidence avec la tangente au cercle issue du projeté sur la droite du centre du cercle (en pointillé).

Prenant maintenant la polaire de ces deux énoncés par rapport à un cercle quelconque nous obtenons que ces deux énoncés restent valables sur une conique quelconque au lieu d'un cercle.

Ci-dessous le théorème de Pascal pour une hyperbole dans une situation « croisée » : non seulement l'hexagone n'est pas convexe, mais les côtés se croisent.

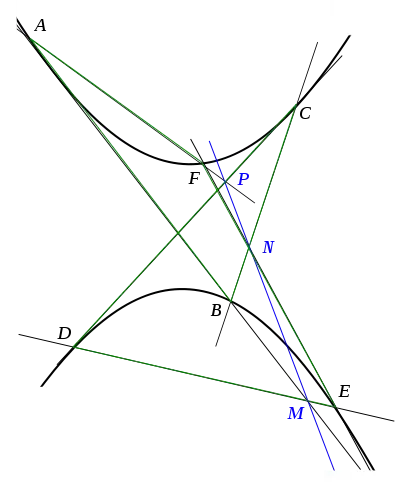
La réciproque de ce théorème est vraie également : si les trois points A, B, C d'intersection des côtés opposés de l'hexagone sont alignés alors l'hexagone est inscrit dans une conique.

Nota bene : dans son texte d'essai, Pascal mentionne cette propriété comme un petit lemme secondaire, on peut supposer qu'il n'avait pas perçu l'aspect fondamental de ce théorème qui est l'un des principaux de la géométrie projective.

Le théorème de Brianchon admet une réciproque qui permet de définir les coniques d'une façon purement formelle en géométrie projective formelle.

Nous en proposons une totalement analytique.

On se donne six points ${\displaystyle A,B,C,A',B',C'}$.

On prend comme repère ${\displaystyle A,B,C}$. Une conique passant par ${\displaystyle A,B,C}$ admet une équation de la forme

${\displaystyle (1)\qquad aX(X-1)+2bXY+cY(Y-1)=0.}$

On note ${\displaystyle \alpha ,\alpha '}$ les coordonnées de ${\displaystyle A'}$ (etc).

${\displaystyle (AB)\cap (B'C')=M}$ a pour ordonnée ${\displaystyle {\frac {\beta \gamma '-\gamma \beta '}{\beta -\gamma }}}$ ;

${\displaystyle (AC)\cap (A'B')=N}$ a pour abscisse ${\displaystyle {\frac {\alpha \beta '-\alpha '\beta }{\beta '-\alpha '}}}$.

Au lieu de calculer les coordonnées de ${\displaystyle (CC')\cap (BA')}$ et de vérifier l'alignement nous dirons que les trois droites ${\displaystyle (MN)}$, ${\displaystyle (CC')}$, et ${\displaystyle (BA')}$ sont concourantes.

Équation de ${\displaystyle (CC')}$ : ${\displaystyle \quad (\gamma -1)Y=\gamma '(X-1)}$ ;

Équation de ${\displaystyle (BA')}$ : ${\displaystyle \,\quad \alpha Y=(\alpha '-1)X+\alpha }$ ;

Équation de ${\displaystyle (MN)}$ :

${\displaystyle \quad {\begin{vmatrix}{\frac {\alpha \beta '-\alpha '\beta }{\beta '-\alpha '}}&0&X\\0&{\frac {\beta \gamma '-\gamma \beta '}{\beta -\gamma }}&Y\\1&1&1\end{vmatrix}}=0={\begin{vmatrix}\alpha \beta '-\alpha '\beta &0&X\\0&\beta \gamma '-\gamma \beta '&Y\\\beta '-\alpha '&\beta -\gamma &1\end{vmatrix}}}$

Le concours des droites se traduit par la nullité du déterminant

${\displaystyle D_{1}={\begin{vmatrix}-\gamma '&1-\alpha '&(\beta '-\alpha ')(\beta \gamma '-\gamma \beta ')\\\gamma -1&\alpha &-(\beta -\gamma )(\alpha \beta '-\alpha '\beta )\\\gamma '&-\alpha &(\beta \gamma '-\gamma \beta )'(\alpha \beta '-\alpha '\beta )\end{vmatrix}}}$

Maintenant, le fait que les points ${\displaystyle A',B',C'}$ soient sur la conique d'équation (1) se traduit par un système de trois équations (une par point) d'inconnues ${\displaystyle a,b,c}$ et qui admet une solution non triviale. Ceci se traduit par la nullité du déterminant

${\displaystyle D_{2}={\begin{vmatrix}\alpha (\alpha -1)&\alpha \alpha '&\alpha '(\alpha '-1)\\\beta (\beta -1)&\beta \beta '&\beta '(\beta '-1)\\\gamma (\gamma -1)&\gamma \gamma '&\gamma '(\gamma '-1)\end{vmatrix}}}$

Ces deux déterminants sont égaux.

On peut bien sûr les calculer par la méthode de Sarrus, mais on peut aussi observer que dans ${\displaystyle D_{2}}$, le terme ${\displaystyle \alpha \alpha '}$ (etc) n'apparaît que dans la deuxième colonne son facteur valant

${\displaystyle {\begin{vmatrix}\beta (\beta -1)&\beta '(\beta '-1)\\\gamma (\gamma -1)&\gamma '(\gamma '-1)\end{vmatrix}}}$

Nous calculons ce facteur dans ${\displaystyle D_{1}}$ en utilisant la deuxième colonne :

• ${\displaystyle \quad (\gamma -1)\beta '(\beta \gamma '-\gamma \beta ')+\gamma '\beta '(\beta -\gamma )}$ pour la première ligne ;
• ${\displaystyle \quad \gamma '(\beta \gamma '-\gamma \beta ')\beta +\gamma '(\beta \gamma '-\gamma \beta ')}$ pour la deuxième ;
• ${\displaystyle \quad \gamma '\beta (\beta -\gamma )+(\gamma -1)(\beta \gamma '-\gamma '\beta )}$ pour la troisième.

La somme donne la même expression que dans ${\displaystyle D_{2}}$.

En échangeant ${\displaystyle \alpha '}$ et ${\displaystyle \gamma }$, ${\displaystyle \beta ,\beta '}$ et ${\displaystyle \alpha ,\gamma '}$ les déterminants ne changent pas ce qui permet d'affirmer l'égalité des coefficients de ${\displaystyle \gamma \gamma '}$.

Reste celui de ${\displaystyle \beta \beta '}$, qui vaut

${\displaystyle \gamma '{\begin{vmatrix}\gamma -1&\alpha \\\gamma '&-\alpha \end{vmatrix}}+\alpha {\begin{vmatrix}\gamma '&1-\alpha '\\\gamma '&-\alpha \end{vmatrix}}+(\alpha \gamma '+\alpha '\gamma ){\begin{vmatrix}-\gamma '&1-\alpha '\\\gamma -1&-\alpha \end{vmatrix}};}$

soit finalement le même que dans ${\displaystyle D_{1}}$ une fois effectué le petit calcul.

Après Pascal, on continue à expliquer et développer ce théorème, ce qui prouve sa pertinence en géométrie projective. Le mathématicien suisse Jakob Steiner (1796-1863) étudie la figure qui s'obtient par la formation d'hexagones de toutes les formes possibles à partir de six points fixes dans une conique, et observe soixante droites de Pascal. Plus tard, en 1828, le même Steiner découvre que les soixante droites de Pascal coïncident, par groupes de trois, en vingt points, appelés points de Steiner.

En 1830, le mathématicien et physicien allemand Julius Plücker (1801-1868) démontre que les points de Steiner sont alignés, quatre par quatre, sur quinze droites appelées droites de Plücker.

Enfin, le théorème est généralisé en 1847 par le mathématicien et astronome allemand August Ferdinand Möbius (1790-1868), connu pour l'invention du ruban de Möbius[2].

 : document utilisé comme source pour la rédaction de cet article.

• Jordi Deulofeu Piquet, Roger Deulofeu Batllori et Philippe Garnier (Trad.), Le fondateur de la théorie des probabilités : Pascal, Barcelone, RBA Coleccionables, 2018, 157 p. (ISBN 978-84-473-9564-4). 

Plan projectif arguésien

• Notice dans un dictionnaire ou une encyclopédie généraliste :

  • Encyclopædia Britannica
• Une démonstration du théorème de Pascal dans le cas général à l'aide des coordonnées barycentriques sur Math Web

• Portail de la géométrie