Théorème de Malus
Le théorème de Malus ou théorème de Malus-Dupin[1], nommé d'après Étienne Louis Malus et Charles Dupin, est un résultat de l'optique ondulatoire.
Énoncés
Le théorème de Malus s'énonce dans le cas général de la manière suivante :
Les surfaces d'ondes sont partout orthogonales aux lignes de champ de .
Dans un milieu isotrope, cela se traduit par :
Les surfaces d'ondes sont partout orthogonales aux rayons lumineux, qui sont les lignes de champ du vecteur de Poynting.
On peut encore le reformuler de la manière suivante :
Les rayons lumineux issus d’une même source ponctuelle, après avoir subi un même nombre de réflexions et de réfractions, sont orthogonaux aux fronts d'ondes[2].
Exemple d'application
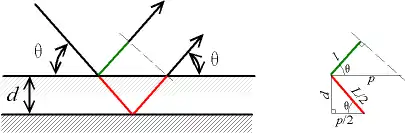
Le théorème de Malus est utilisé pour calculer la différence de marche entre deux rayons lumineux. Le schéma ci-contre représente un interféromètre de Michelson en configuration de lame d'air. Après « repliement » de l'interféromètre, on obtient un miroir fictif parallèle à un miroir réel. Ici sont représentés deux rayons confondus, un réel se réfléchissant dans le miroir réel et un fictif se réfléchissant dans le miroir fictif. Le théorème de Malus ne permet pas d'affirmer que la droite tracée en pointillés gris sur le schéma, étant orthogonale aux deux rayons, est une surface d'onde (car le rayon rouge subit deux réfractions pour une réflexion et le rayon vert seulement une réflexion). Cependant si on considère le principe du retour inverse de la lumière, dans le cas hypothétique d'une source à l'infini dans la direction des flèches alors le théorème de Malus permet de dire que la droite tracée en pointillés gris sur le schéma est une surface d'onde pour cette source hypothétique. Le calcul de la différence de marche entre ces deux rayons se résume alors à la différence de longueur entre les lignes rouge et verte.
Références
- Pérez, José-Philippe., Optique : fondements et applications avec 200 exercices et problèmes résolus, Paris/Milan/Barcelone, Masson, (ISBN 2-225-85213-8 et 978-2-225-85213-8, OCLC 35844465, lire en ligne), p. 16
- http://scienceworld.wolfram.com/physics/MalusandDupinTheorem.html