Spirale de Fermat
Une spirale de Fermat est une courbe plane d'équation polaire: Son nom est une référence au mathématicien Pierre de Fermat qui la décrit dans une lettre à Marin Mersenne en 1636 et présente sa propriété d'aire balayée par un rayon[1]. Cette courbe a aussi été étudiée par Pierre Varignon[2] en 1704 dans le cadre de son étude générale des spirales d'équation polaire .

Propriétés géométriques

La spirale de Fermat est une courbe transcendante qui possède deux branches (pour ρ positif et pour ρ négatif) symétriques par rapport à O. Elle partage le plan en deux composantes connexes[3].
Pour tout point M de la courbe, on appelle T et N les points d'intersection de la tangente et la normale à la courbe en M avec la droite passant par O et perpendiculaire à (OM). Les longueurs OT et ON (sous-tangente et sous-normale) valent alors[4]: et L'aire du triangle OMN est donc constante égale au quart du carré de côté a.
L'aire balayée par le rayon OM de Md à Mf est donnée par la formule[4]:

En particulier, si l'on prend pour θk la valeur 2kπ, la surface balayée par le rayon de M0 à M1 correspond à la moitié de l'aire du disque de rayon OM1, les autres spires ont des aires identiques égales à l'aire du disque de rayon OM1[4]. C'est la propriété énoncée par Fermat en 1636[1].
Le rayon de courbure s'exprime par[4]: La courbe possède donc un seul point d'inflexion à l'origine.
Son abscisse curviligne est donnée par[3],[4]: et la rectification de la courbe fait intervenir une intégrale elliptique de première espèce[4].
Relation avec d'autres courbes
La spirale de Fermat est l'image par une inversion, de pôle O et de cercle de rayon a, du lituus[3] d'équation polaire ρ²θ = a².
Si on fait rouler la spirale de Fermat d'équation ρ² = a²θ sur la courbe d'équation , son centre se déplace sur l'axe des abscisses[3]. Cette propriété avait déjà été remarquée par Pierre Varignon en 1704[5].
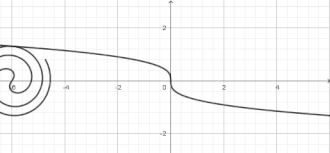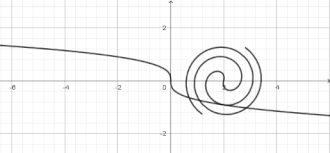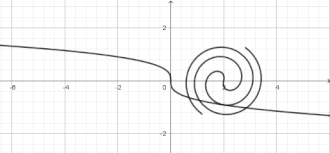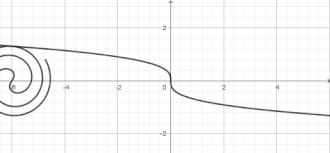
Modélisation

La spirale de Fermat peut servir à modéliser l’implantation des fleurs du tournesol : Helmut Vogel en 1979[6] a remarqué que les points de coordonnées polaires et simulait assez fidèlement la fleur de tournesol[7]. Or ces points sont situés sur la spirale de Fermat d'équation où φ est le nombre d'or et l'angle est l'angle d'or. Cette modélisation reste cependant une simplification d'une phyllotaxie plus complexe[8].
D'autres[9],[10] l'ont utilisée pour modéliser le taijitu du Yin et Yang en limitant la courbe d'équation ρ² = θ au cercle de rayon 1.
Notes et références
- Lettre de Fermat à Mersenne du 3 juin 1636, dans Paul Tannery, Œuvres de Fermat, T. III, p; 277, lire en ligne
- Varignon 1704.
- Mathcurve.
- Teixeira 1909.
- Varignon 1704, p. 84.
- Helmut Vogel (1979). «A better way to construct the sunflower head». Mathematical Biosciences, Juin 1979, vol. 44 , pp 179–189, Présentation en ligne
- Øyvind Hammer, The Perfect Shape: Spiral Stories, Springer, 2016, p.50(aperçu en ligne)
- Massimiliano Sassi Teva Vernoux, «Auxin and self-organization at the shoot apical meristem», Journal of Experimental Botany, Volume 64, numero 9, 1 Juin 2013, Pages 2579–2592, https://doi.org/10.1093/jxb/ert101 - Lire en ligne
- Serge Cantat, Le Yin et le Yang, 4 mars 2011, sur Image des mathématiques (CNRS)
- Taras Banakh, Oleg Verbitsky, Yaroslav Vorobets, «Fermat's spiral and the line between Yin and Yang», American Mathematical Monthly, nov. 2010 - Présentation en ligne
Bibliographie
- Pierre Varignon, « Nouvelle formation des spirales - exemple II », Mémoire de l'académie des sciences de l'Institut de France, , p. 94 - 103 (lire en ligne).
- Francisco G. Teixeira, Obras sobre Mathematica : Traité des courbes spéciales remarquables planes et gauches, vol. V, Coimbra, Imprensa da Universidade, (lire en ligne), p. 67-68.
- Robert Ferreol, « Spirale de Fermat », sur Encyclopédie des formes mathématiques remarquables, (consulté le )
- Portail de la géométrie