Séries de Minggatu
En mathématiques, les séries de Minggatu sont des développements en série de fonctions trigonométriques découverts vers 1730 par Minggatu, un mathématicien mongol au service des empereurs de la dynastie Qing. Ses résultats, parmi lesquels figure la découverte des nombres de Catalan, s'inspirent des travaux des mathématiciens européens, mais sont obtenus par des méthodes géométriques et algébriques totalement indépendantes des leurs ; ils ont été publiés (après sa mort) dans son ouvrage majeur, le Geyuan Milu Jifa (Méthode rapide pour obtenir les divisions exactes d'un cercle).

Contexte historique
En 1701, le missionnaire jésuite Pierre Jartoux (1669-1720) vint en Chine, apportant avec lui trois développements en série de fonctions trigonométriques dus à Isaac Newton et James Gregory[1] :
Ces séries suscitèrent un grand intérêt parmi les mathématiciens chinois, le calcul de par ces « méthodes rapides » ne demandant que des multiplications et des divisions, et s'avérant beaucoup plus efficace que les calculs à l'aide de racines carrées de l'algorithme classique de Liu Hui (en). Cependant, Jartoux n'expliqua pas la méthode employée pour construire ces séries, et Minggatu le soupçonna de ne pas vouloir en partager le secret. Il travailla par intermittence sur ce problème durant trente années, et obtint un modèle géométrique de construction de séries trigonométriques, qui lui permit non seulement de retrouver les trois séries précédentes, mais également six autres, découvrant au passage et utilisant les nombres de Catalan, au moins 20 ans avant les mathématiciens européens.
Un exemple de calcul de séries : la méthode des deux segments
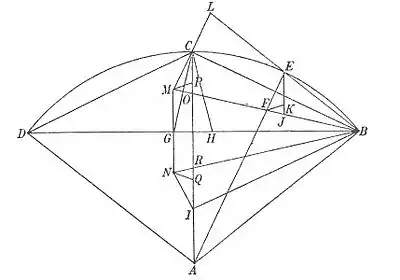
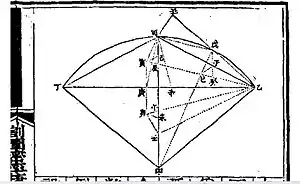
La construction ci-contre (figure 2) illustre la méthode de Minggatu. L'arc BCD est une portion du cercle unité (de centre A) ; on pose BC = CD = x ; construisant des triangles isocèles BGC et DCH, on a BD = 2x-GH[2]. On pose alors EJ = EF, FK = FJ et on prolonge BE jusqu'en L tel que EL = BE ; de même, on prolonge BF jusqu'à M avec BF = MF. L, M et C sont alignés. Posant BI = BC, on a les proportionnalités
On obtient de même une série de triangles semblables ABE, BEF, FJK, BLM, CMO, MOP, CGH et de plus les triangles CMO et EFJ sont égaux[3], aussi
- ,
- donc
- , d'où
- ,
- et .
ABEC et BLIN étant semblables[3],
- et
- Posant
- , et .
Finalement [4], des manipulations algébriques amènent à
et plus généralement (en itérant la construction) :
- [5].
Éliminant les termes en sauf le premier et le dernier, on aboutit à
Les coefficients des numérateurs : 1, 1, 2, 5, 14, 42, 132 ...... (voir la figure 1) sont les nombres de Catalan ; Minggatu est le premier à les avoir décrits[6],[7].
Ainsi[8] :
où est un nombre de Catalan. Minggatu introduisit ainsi l'usage de relations de récurrence dans les mathématiques chinoises[11], montrant en particulier que .
Si, dans la figure 2, on pose l'angle , on a alors ; les relations précédentes permettent alors à Minggatu d'en déduire la relation :
(cette dernière formule se démontre aisément à l'aide de la série génératrice découverte par Euler 20 ans plus tard : ).


La limite quand le nombre de segments augmente
Par des calculs analogues, Minggatu obtient des séries correspondant à des décompositions en n= 3, 5, 10, 100, 1000 et 10000 segments[12] ; il en déduit (de manière empirique) la série correspondant au cas limite quand n tend vers l'infini. Ainsi, il réécrit
..........
..............
..................
(où les y sont les longueurs de la corde et les a les longueurs des segments subdivisant l'arc) et remarque que les dénominateurs 24.000000240000002400,24.000002400000218400*80 approchent 24 et 24*80 respectivement, tandis que n*a (100a, 1000a, 10000a) tend vers la longueur de l'arc ; ainsi [8],[13]
- .....
Par inversion de séries, il exprime enfin l'arc en fonction de la corde[13] :
- ............
Notes
- (en) He Shaodong, "A Key Problem in the Study of Infinite Series", in The Qing Dynasty, Studies in the History of Natural Sciences, vol 6, n°3, 1989 ; pp 205–214
- (en) Li Yan, Selected Papers in History of Chinese Mathematics, livre III, "Li Yan Qian Baocong History of Science Collection" Volume 7, 300
- Luo 1998, p. 96
- Luo 1998, p. 100
- Luo 1998, p. 106
- (en) Jianjin Luo, Ming Antu and his power series expansion, Mathematical Journal 34 volume 1, pp. 65-73
- (en) Peter Larcombe, The 18th Century Chinese Discovery of Catalan Numbers, Mathematical Spectrum, Vol 32, No 1, pp5-7, 1999/2000
- En toute rigueur, il faudrait démontrer que le dernier terme tend vers 0 (et plus généralement que les limites devinées sont correctes), mais outre que Minggatu ignore les idées du calcul infinitésimal, ces questions de limite sont traitées le plus souvent sans aucune rigueur en Europe à cette époque.
- Luo 1998, p. 113
- (en) Yan Xue-min et Luo Jian-jin, Catalan Numbers, A Geometric Model, Journal of Zhengzhou Univ Vol 38 No2, juin 2006, p. 22
- Luo 1998, p. 114
- Mikami 1913, p. 147
- Mikami 1913, p. 148
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Ming Antu's infinite series expansion of trigonometric functions » (voir la liste des auteurs).
- (zh) Jianjin Luo, 明安图原著 罗见今译注 《割圆密率捷法》 内蒙古教育出版社 [« Une traduction moderne du Geyuan Milu Jifa de Minggatu, annotée par Luo Jianjin »], Inner Mongolia Education Press, (ISBN 7-5311-3584-1)C'est la seule édition moderne, avec des notes transcrivant l'ouvrage en notation mathématique usuelle.
- (en) Yoshio Mikami, The Development of Mathematics in China and Japan, Bibliothèque du Congrès, 61-13497,
- Portail de l'analyse