Q-learning
En intelligence artificielle, plus précisément en apprentissage automatique, le Q-learning est une technique d'apprentissage par renforcement. Cette technique ne nécessite aucun modèle initial de l'environnement. La lettre 'Q' désigne la fonction qui mesure la qualité d'une action exécutée dans un état donné du système[1].
Description
Cette méthode d'apprentissage permet d'apprendre une politique, qui indique quelle action effectuer dans chaque état du système. Cela fonctionne par l'apprentissage d'une fonction de valeur état-action notée qui permet de déterminer le gain potentiel, c'est-à-dire la récompense sur le long terme, , apporté par le fait d'effectuer une certaine action dans un certain état en suivant une politique optimale. Lorsque cette fonction de valeur d'action-état est connue/apprise par l'agent, la politique optimale peut être construite en sélectionnant l'action à valeur maximale pour chaque état, c'est-à-dire en sélectionnant l'action qui maximise la valeur quand l'agent se trouve dans l'état .
Un des points forts du -learning est qu'il permet de comparer les récompenses probables de prendre les actions accessibles sans avoir de connaissance initiale de l’environnement. En d'autres termes, bien que le système soit modélisé par un processus de décision markovien (fini), l'agent qui apprend ne le connait pas et l'algorithme du -learning ne l'utilise pas.
Cette notion d’apprentissage par récompense a été introduite à l'origine dans la thèse de Watkins en 1989[2]. C'est une variante de l'apprentissage par différence temporelle[3]. Par la suite, il a été prouvé, que le -learning converge vers une politique optimale, c'est-à-dire qu'il conduit à maximiser la récompense totale des étapes successives[4].
Algorithme
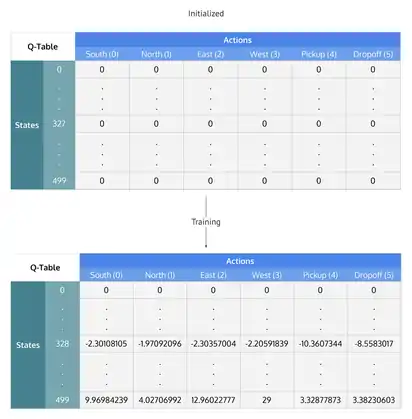
La situation consiste en un agent, un ensemble d'états et d'actions . En réalisant une action , l'agent passe d'un état à un nouvel état et reçoit une récompense (c'est une valeur numérique). Le but de l'agent est de maximiser sa récompense totale. Cela est réalisé par apprentissage de l'action optimale pour chaque état. L'action optimale pour chaque état correspond à celle avec la plus grande récompense sur le long terme. Cette récompense est la somme pondérée de l'espérance mathématique des récompenses de chaque étape future à partir de l'état actuel. La pondération de chaque étape peut être où est le délai entre l'étape actuelle et future et un nombre compris entre 0 et 1 (autrement dit ) appelé facteur d'actualisation.
L'algorithme calcule une fonction de valeur action-état :
Avant que l'apprentissage ne débute, la fonction est initialisée arbitrairement. Ensuite, à chaque choix d'action, l'agent observe la récompense et le nouvel état (qui dépend de l'état précédent et de l'action actuelle). Le cœur de l'algorithme est une mise à jour de la fonction de valeur. La définition de la fonction de valeur est mise à jour à chaque étape de la façon suivante[5] :
où est le nouvel état, est l'état précédent, est l'action choisie, est la récompense reçue par l’agent, est un nombre entre 0 et 1, appelé facteur d'apprentissage, et est le facteur d'actualisation.
Un épisode de l'algorithme finit lorsque est un état final. Toutefois, le -learning peut aussi être appliqué à des tâches non épisodiques. Si le facteur d'actualisation est plus petit que 1, la valeur action-état est finie même pour infini.
N.B. : Pour chaque état final , la valeur de n'est jamais mise à jour et maintient sa valeur initiale. Généralement, est initialisé à zéro.
Pseudo-code
Voici le pseudo-code du Q-learning.
initialiser Q[s, a] pour tout état s, toute action a de façon arbitraire, mais Q(état terminal, a) = 0 pour toute action a
répéter
//début d'un épisode
initialiser l'état s
répéter
//étape d'un épisode
choisir une action a depuis s en utilisant la politique spécifiée par Q (par exemple ε-greedy)
exécuter l'action a
observer la récompense r et l'état s'
Q[s, a] := Q[s, a] + α[r + γ maxa' Q(s', a') - Q(s, a)]
s := s'
a := a'
jusqu'à ce que s soit l'état terminal
Influence des variables sur l'algorithme
Facteur d'apprentissage
Le facteur d'apprentissage détermine à quel point la nouvelle information calculée surpassera l'ancienne. Si = 0, l'agent n'apprend rien. A contrario, si = 1, l'agent ignore toujours tout ce qu'il a appris et ne considèrera que la dernière information.
Dans un environnement déterministe, la vitesse d'apprentissage est optimale. Lorsque le problème est stochastique, l'algorithme converge sous certaines conditions dépendant de la vitesse d'apprentissage. En pratique, souvent cette vitesse correspond à pour toute la durée du processus[6].
Facteur d'actualisation
Le facteur d'actualisation γ détermine l'importance des récompenses futures. Un facteur 0 rendrait l'agent myope en ne considérant seulement les récompenses courantes, alors qu'un facteur proche de 1 ferait aussi intervenir les récompenses plus lointaines. Si le facteur d'actualisation est proche ou égal à 1, la valeur de peut diverger[7].
Extensions et variantes
Double Q-learning
Comme le Q-learning utilise l'estimateur max, le Q-learning surestime la valeur des actions et de fait, dans des environnements bruités, l'apprentissage est lent. Ce problème est résolu dans la variante appelée double Q-learning[8] qui utilise deux fonctions d'évaluation et apprises sur deux ensembles d'expériences différents. La mise à jour se fait de façon croisée :
- , et
Comme la valeur estimée est évaluée en utilisant une autre politique, le problème de la surestimation est résolu. L'apprentissage de l'algorithme à ensemble peut être effectué en utilisant des techniques d'apprentissage profond, ce qui donne les réseaux DQN (deep Q-networks, réseaux profonds Q). On peut alors avoir le Double DQN, pour obtenir de meilleures performances qu'avec l'algorithme DQN original[9].
Notes et références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Q-Learning » (voir la liste des auteurs).
- Tambet Matiisen, « Demystifying Deep Reinforcement Learning | Computational Neuroscience Lab », sur neuro.cs.ut.ee, (consulté le )
- C. J. Watkins, Learning from delayed rewards, Kings College, Cambridge, mai 1989
- (en) George F Luger, Artificial intelligence : Structures and strategies for complex problem solving. 5e édition., Addison Wesley, , 903 p. (ISBN 0-321-26318-9, lire en ligne), p. 448
- Watkins et Dayan, Q-learning.Machine Learning, 1992
- (en) David L. Poole et Alan K. Mackworth, Artificial Intelligence, Cambridge University Press, (ISBN 978-0-511-79479-7, DOI 10.1017/CBO9780511794797, lire en ligne), p. 469
- Reinforcement Learning: An Introduction, Richard Sutton et Andrew Barto, MIT Press, 1998.
- (en) Stuart J. Russell et Peter Norvig, Artificial Intelligence : A Modern Approach, Prentice Hall, , Third éd., 1132 p. (ISBN 978-0-13-604259-4), p. 649
- Hado van Hasselt, « Double Q-learning », Advances in Neural Information Processing Systems, vol. 23, , p. 2613–2622 (lire en ligne [PDF])
- Hado van Hasselt, Arthur Guez et David Silver, « Deep reinforcement learning with double Q-learning », AAAI Conference on Artificial Intelligence, , p. 2094–2100 (lire en ligne [PDF])
- Portail de l’éducation