Plan affine
En géométrie le concept de plan affine a été inventé pour pouvoir parler de droites parallèles sans s'encombrer de notions métriques telles que la distance entre deux points ou l'angle entre deux droites. L'approche axiomatique ne présuppose pas la notion d'espace vectoriel, de plan vectoriel en l'occurrence, ni celle de corps commutatif. Cependant ces deux dernières notions sont sous-jacentes (voir plan affine de Desargues).
Axiomes du plan affine
Un plan affine vérifie les axiomes
- Il existe au moins 2 points.
- Chaque droite possède au moins 3 points.
- Pour deux points distincts il existe une et une seule droite qui leur est incidente.
- Pour toute droite il existe au moins un point non incident à cette droite.
- Étant donnée une droite g et un point P non incident à g, il existe une et une seule droite h qui soit incidente à P et qui n'ait pas de point commun avec g. Vocabulaire: les droites g et h sont dans ce cas dites strictement parallèles. Une droite est simplement parallèle avec elle-même, elle n'est pas strictement parallèle avec elle-même. Si deux droites sont simplement parallèles on dit qu'elles ont la même direction.
- Axiome de Pappus affine : Si les points A, E, C sont alignés, si les points B, D, F sont alignés sur une autre droite, si (AB)//(DE) et si (BC)//(EF) alors (FA)//(CD).
Relation d'équivalence
Le parallélisme simple entre deux droites est une relation d'équivalence (réflexive, symétrique, transitive). Le parallélisme strict ne l'est pas, il manque la réflexivité. L'ensemble-quotient des droites par la relation de parallélisme-simple s'appelle l'ensemble des directions du plan affine.
Parallélogramme
Définition affine du parallélogramme : un parallélogramme général est la figure formée par deux paires de droites simplement parallèles.
- Un parallélogramme strict est un polygone formé par deux paires de droites strictement parallèles, chaque paire n'ayant pas la même direction.
- Un parallélogramme aplati est formé d'une paire de droites strictement parallèles et d'une paire de droites confondues.
- Un parallélogramme-point est formé de deux paires de droites confondues.
Transformations intéressantes
Translation
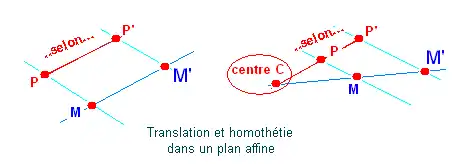
Soient deux points P et P', distincts ou confondus.
Définition. La translation selon P et P' est la transformation qui transforme le point M en M' tel que les paires de droites {(PP')(MM')}, {(PM)(P'M')} forment un parallélogramme.
Propriétés simples des translations.
- La translation nulle existe, elle a lieu quand les deux points de référence P et P' sont confondus. Les translations forment un groupe abélien.
- Théorème de croisement des translations : si M' est l'image de M par la translation selon P et P', alors M' est l'image de P' par la translation selon P et M.
 .
.
Homothétie
Soient trois points alignés C, P et P', avec P distinct de C.
Définition : On appelle homothétie de centre C et selon PP' la transformation qui à tout point M associe un point M' tel que 1) CMM' soient alignés et 2) que les droites (PM) et (P'M') soient parallèles.
Dilatations
L'ensemble réunion des translations et des homothéties est parfois appelé l'ensemble des dilatations du plan affine (à ne pas confondre avec Dilatation (géométrie)). On peut démontrer que c'est un groupe.
Bibliographie
- Fritz Reinhardt et Heinrich Soeder (trad. de l'allemand), Atlas des mathématiques, Paris, Le Livre de poche, coll. « La Pochothèque », (1re éd. 1974), 502 p. (ISBN 2-253-13013-3), p. 139.

- (en) Emil Artin, Geometric algebra, John Wiley & Sons, coll. « Wiley Classics Library », (1re éd. 1957), 224 p. (ISBN 978-1-118-16454-9, lire en ligne)
Voir aussi
- Géométrie affine
- Espace affine
- Théorème de Pappus pour la version projective du théorème (ou de l'axiome)
- Portail de la géométrie
