Néphroïde

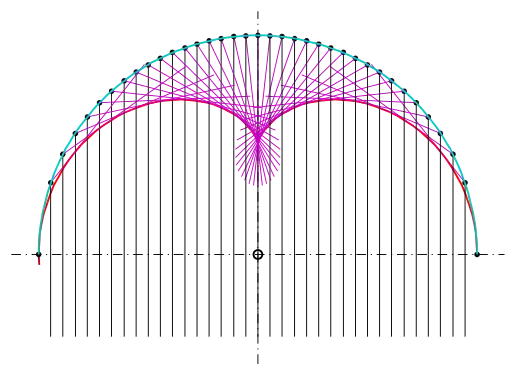
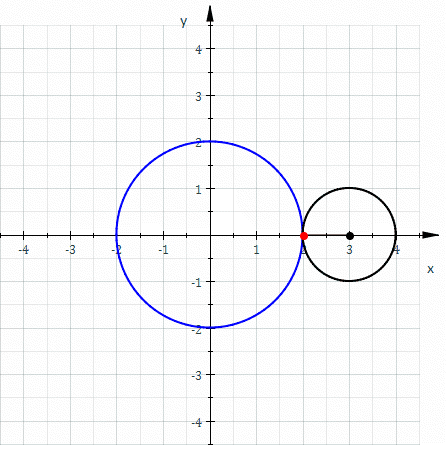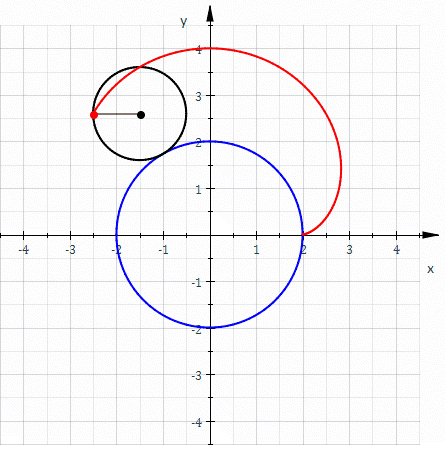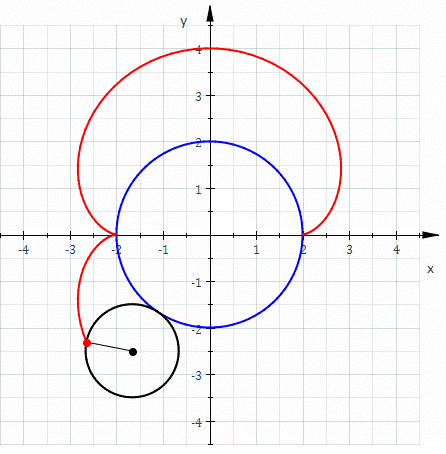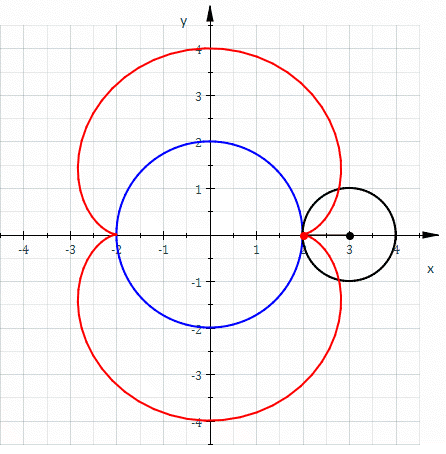
La néphroïde est une courbe algébrique plane, trajectoire d'un point fixé à un cercle qui roule sans glisser sur un second cercle de diamètre double. C'est donc un cas particulier d'épicycloïde, à deux rebroussements. Un épicycloïde est une courbe cycloïdale dont la directrice est un cercle.

Construction mécanique de la néphroïde

Étymologie et histoire

Son nom vient du grec nephros (rein), en référence à sa forme, et lui fut donné par Richard Proctor.

Ce type de courbe a été étudié par Huygens, Tschirnhausen en 1679, Jacques Bernoulli en 1692, Daniel Bernoulli en 1725 et Proctor qui a donné le nom en 1878.

Définition mathématique

La courbe peut être définie par l'équation cartésienne suivante :

(x^{2}+y^{2}-4a^{2})^{3}=108a^{4}y^{2}

On peut également la définir par une équation paramétrique :

x=a(3\cos t-\cos 3t),\quad y=a(3\sin t-\sin 3t).

Optique

La néphroïde est une caustique de cercle par réflexion avec la source lumineuse située infiniment loin, de sorte que les rayons incidents sont parallèles. Lorsque la source est située sur le bord du cercle, on distingue une forme comparable mais il s'agit alors d'une cardioïde.

Cardioïde apparaissant nettement dans une cocotte en fonte
Semi-néphroïde comme caustique. La source lumineuse est située infiniment loin vers le bas de la figure.

Références

Note sur la néphroïde de Proctor, par F. Balitrand, in Nouvelles annales de mathématiques (1915).

Voir aussi

Liens externes

Portail de la géométrie

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.