Multi-arbre

En combinatoire et en théorie des ordres, le terme multi-arbre peut décrire l'une des deux structures suivantes : un graphe orienté acyclique dans lequel l'ensemble des sommets accessibles à partir d'un nœud est toujours un arbre, ou un ensemble partiellement ordonné dans lequel il n'existe pas quatre éléments a, b, c, et d qui forment un sous-ordre en diamant, avec a ≤ b ≤ d et a ≤ c ≤ d mais où b et c sont incomparables (un tel ensemble ordonné est aussi appelé diamond-free poset (ou ordre partiel sans diamant)[1].

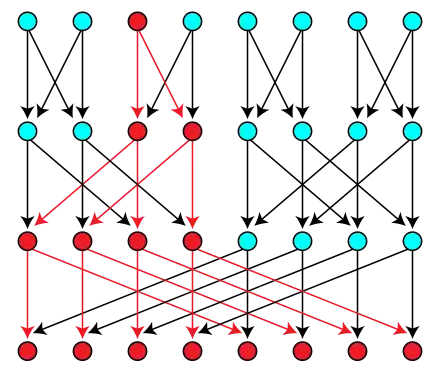
Un réseau papillon, un multi-arbre utilisé en calcul distribué, montrant (en rouge) le sous-arbre accessible à partir d'un de ses nœuds.

Équivalence entre les définitions

Si G est un graphe orienté acyclique (un DAG) dans lequel les nœuds accessible à partir d'un sommet forment un arbre (ou, de manière équivalente, si G est un graphe orienté dans lequel il existe au moins un chemin entre deux nœuds) alors la relation d'accessibilité dans G est un ordre partiel sans diamant. Réciproquement, si P est un ordre partiel sans diamant, sa réduction transitive forme un graphe orienté acyclique dans lequel les descendants d'un nœud forment un arbre.

Familles sans diamant

Une famille d'ensembles est une famille F d'ensemble pour lequel l'ordre d'inclusion est sans diamant. Notons la plus grande famille de parties sans diamant d'un ensemble à n éléments, on a

et il est conjecturé[1] que la limite est 2.

Applications

Les multi-arbres peuvent être utilisés pour représenter des taxonomies multiples chevauchantes sur un même ensemble[2].

Si un arbre généalogique contient des mariages multiples entre deux familles mais sans mariage entre may contain multiple marriages from one family to another, but does not contain marriages between any parents de sang, il prend la forme d'un multi-arbre[3]. Dans le contexte de la théorie de la complexité, les multi-arbres ont aussi été appelés « graphes fortement inambigus » ou « mangroves »; ils seervent à modéliser les algorithmes non déterministes où il existe au plus un chemin de calcul qui connecte deux états[4]

Structures voisines

Un polyarbre est un graphe orienté acyclique obtenu en orientant chaque arête d'un arbre (théorie des graphes) ; c'est un cas particulier d'un multi-arbre.

L'ensemble des nœuds connecté à un nœud donné u dans un multi-arbre est une arborescence.

Le mot « multitree » a aussi été utilisé pour désigner un ordre partiel série parallèle (en)[5].

Notes et références
  1. Jerrold R. Griggs, Wei-Tian Li et Linyuan Lu, « Diamond-free families », Journal of Combinatorial Theory, Series A, vol. 119, no 2,‎ , p. 310–322 (DOI 10.1016/j.jcta.2011.09.002).
  2. George W. Furnas et Jeff Zacks, « Multitrees: enriching and reusing hierarchical structure », Proc. SIGCHI conference on Human Factors in Computing Systems (CHI '94),‎ , p. 330–336 (DOI 10.1145/191666.191778).
  3. Michael J. McGuffin et Ravin Balakrishnan, « Interactive visualization of genealogical graphs », IEEE Computer Society, Los Alamitos, CA, USA,‎ , p. 3–3 (DOI 10.1109/INFOVIS.2005.22).
  4. Eric Allender et Klaus-Jörn Lange, « StUSPACE(log n) ⊆ DSPACE(log2 n/log log n) », Springer-Verlag, vol. 1178,‎ , p. 193–202 (DOI 10.1007/BFb0009495).
  5. Heinz Adolf Jung, « On a class of posets and the corresponding comparability graphs », Journal of Combinatorial Theory, Series B, vol. 24, no 2,‎ , p. 125–133 (DOI 10.1016/0095-8956(78)90013-8, Math Reviews 0491356).
  • Portail des mathématiques
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.