Monocorde
Le monocorde est un instrument de mesure des intervalles des gammes musicales. Il est constitué d'une caisse de résonance sur laquelle une corde tendue entre deux sillets est divisée par un chevalet mobile. Les rapports de distances entre les différentes partitions de la corde construisent de la sorte une échelle musicale.
Histoire
Boèce attribue l'invention du monocorde en tant qu'instrument expérimental à Pythagore[réf. souhaitée], mais il existait probablement avant en Égypte[1].
Pythagore a fait la démonstration que la hauteur , du son est inversement proportionnelle à la longueur de la corde[réf. nécessaire]. De cette expérience, Pythagore tire les conclusions suivantes :
- En plaçant le chevalet au milieu de la corde — donc, en divisant celle-ci en deux parties égales —, la corde en question fait entendre l'octave supérieure du son de la corde "à vide" (c'est-à-dire non divisée) alors que les mise en vibration des deux parties égales de la corde situées de part et d'autre du chevalet, fait entendre l'unisson.
- De la même façon, en plaçant le chevalet au tiers de la corde — donc, en divisant celle-ci en trois —, la corde en question donne alors le redoublement de la quinte supérieure du son initial (autrement dit, la « douzième supérieure »). De l'autre côté du chevalet, avec une longueur de , on obtient "tout naturellement" la quinte supérieure du son initial.
Théorie
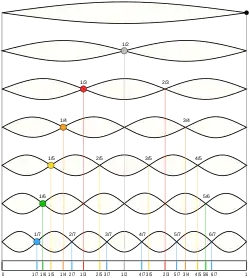
En divisant la corde en intervalles égaux de 2 à 6 on obtient les principaux accords purs[1] :
- par 2 : c'est l'octave supérieure par rapport à la corde entière (rapport de hauteur 2/1) ;
- par 3 : c'est la quinte (rapport de hauteur 3/2, c'est-à-dire qu'on multiplie la fréquence de la fondamentale par 3/2 pour obtenir celle de la quinte : si la longueur = 2/3, alors la hauteur = 1/L = 3/2)
- par 4 : c'est la quarte (rapport 4/3) ;
- par 5 : c'est la tierce majeure (rapport 5/4) ;
- par 6 : c'est la tierce mineure (rapport 6/5).
Soit la longueur de la corde, et sa fréquence ; Pythagore a donc remarqué[réf. nécessaire]que .
On remarque aussi que
Comme , la pratique arithmétique grecque fait noter les nombres rationnels plus grands que 1 comme 1 + X.
En posant , on obtient
d'où on déduit , la notation revient donc à nommer X, depuis X = 0 pour le do à X=1 pour le do de l'octave supérieur.
On déduit aussi :
et
Pour un donné, on voit que la corde est partagée en deux longueurs : et
Or
Par exemple, si la corde à vide donne un Do, le Sol a pour fréquence N = No (1 + 1/2). Il se joue donc avec la frette au [(1/2/(1+1/2)]=1/3 de la longueur.
Les sept notes de la gamme correspondaient à des rationnels "simples" et approximatifs d'une assonance.
Le tableau ci-après donne les valeurs X, encadrant 1+1/2 == 1+5/10(qu'on pourra réduire aisément) et les écarts (rapport de fréquences de deux notes consécutives) ; il apparaît que ces écarts ne sont évidemment pas constants, et il y a un problème à régler simplement l'écart entre les notes (l'écart musical , irrationnel, conduira à la crise majeure des mathématiques, appelée crise pythagoricienne).
| Note | do | ré | mi | fa | sol | la | si | do | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| X | 0 | 1/8 | 1/4 | 1/3 | 1/2 | 2/3 | 7/8 | 1 | ||||||||
| 1 + X | 1 | 1 + 1/8 | 1 + 2/8 | 1 + 3/9 | 1 + 5/10 | 2 - 3/9 | 2 - 1/8 | 2 | ||||||||
| Rapport | 1 | 9/8 | 5/4 | 4/3 | 3/2 | 5/3 | 15/8 | 2 | ||||||||
| Ecarts | 9/8 | 10/9 | 9/8 | 10/9 | 9/8 | |||||||||||
Voir aussi
Articles connexes
Bibliographie
- Claude Abromont et Eugène de Montalembert, Guide de la théorie de la musique, Librairie Arthème Fayard et Éditions Henry Lemoine, coll. « Les indispensables de la musique », , 608 p. [détail des éditions] (ISBN 978-2-213-60977-5)
- Portail de la musique
- Portail de la musique classique
- Portail des musiques du monde