Lois de Cassini
Les lois de Cassini sont trois énoncés qui fournissent une description succincte du mouvement de la Lune. Elles ont été établies en 1693 par Jean-Dominique Cassini, vérifiées par Tobias Mayer et dégagées des publications de Cassini par Félix Tisserand[1] en 1891.
Pour les articles homonymes, voir Cassini.
Ces lois ont été perfectionnées pour prendre en compte les librations et généralisées pour s'appliquer à d'autres satellites et planètes[2],[3].
Lois
- « La Lune tourne sur elle-même, dans le sens direct, d’un mouvement uniforme autour d’un axe dont les pôles sont fixes à sa surface ; la durée de la rotation, 27j 7h 43m 11,5s est identique à la révolution sidérale de la Lune autour de la Terre[4] ;
- l’axe de rotation fait un angle constant avec l’écliptique ; cet angle est de 88˚ 25’ ;
- l’axe de l’écliptique, l’axe de l’orbite de la Lune et son axe de rotation sont constamment dans un même plan[1]. »
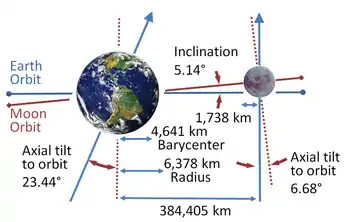
L'axe de rotation de la Lune fait un angle de 1,54 degré avec le pôle de l'écliptique. La normale[5] au plan orbital est orientée du côté opposé à l'axe de rotation par rapport à la normale à l'écliptique, d'un angle de 5,14° (en moyenne, car l'inclinaison oscille légèrement). Les axes orbital et de rotation font donc un angle (à peu près) constant de 6,68°.
Par conséquent, la normale au plan orbital et celle à l'axe de rotation ont la même période de précession par rapport au pôle de l'écliptique ; cette période est de 18,6 années et le mouvement est rétrograde.
États
On dit d'un système qui obéit aux lois de Cassini qu'il est dans un « état de Cassini », c'est-à-dire que l'axe de rotation, la normale à l'orbite et la normale au plan de Laplace sont coplanaires, tandis que l'obliquité demeure constante[2],[3],[6]. Le plan de Laplace est défini comme le plan autour duquel l'orbite d'un satellite ou d'une planète ont une précession avec une inclinaison constante.
Bibliographie
- Paul Brouzeng et Suzanne Débarbat, Sur les traces des Cassini : astronomes et observatoires du sud de la France, Éditions du CTHS, 2001, 360 p.
- Jean-Dominique Cassini, De l’origine et du progrès de l’astronomie, et de son usage dans la géographie et dans la navigation, 1693
- (en) William M. Kaula (en), Introduction to planetary physics : the terrestrial planets, 1968
- (en) Donald H. Eckhardt, « Theory of the Libration of the Moon », Springer Netherlands, vol. 25, , p. 3–49 (DOI 10.1007/BF00911807, Bibcode 1981M&P....25....3E)
- Nicolas Rambaux, « La rotation de la Lune et les lois de Cassini dans le système solaire » — Présentation d'introduction
Compléments
Notes et références
- Félix Tisserand, Traité de mécanique céleste. Théorie de la figure des corps célestes et de leur mouvement de rotation (t. 2 du Traité), 1891, p. 444.
- (en) Stanton J. Peale, « Generalized Cassini's Laws », The Astronomical Journal, vol. 74, , p. 483 (ISSN 0004-6256, DOI 10.1086/110825, Bibcode 1969AJ.....74..483P).
- (en) Marie Yseboodt et Jean-Luc Margot, « Evolution of Mercury's obliquity », Icarus, vol. 181, no 2, , p. 327–337 (ISSN 0019-1035, DOI 10.1016/j.icarus.2005.11.024, Bibcode 2006Icar..181..327Y, lire en ligne).
- La résonance orbitale est de 1:1 : le rapport rotation–orbite est tel que notre satellite présente toujours la même face à la Terre.
- « Normale », sens 7.
- (en) Y. Calisesi, Solar Variability and Planetary Climates, Dordrecht, Springer, , 472 p. (ISBN 978-0-387-48339-9 et 0-387-48339-X, lire en ligne), p. 34