Loi de mélange pour la viscosité

Approximations pour la viscosité de l'air.

La théorie cinétique des gaz permet d'obtenir rigoureusement la viscosité d'un mélange gazeux comme la solution d'un système linéaire[5]^,[6]. Celle-ci peut être écrite comme le quotient de deux matrices. Les solutions approchées sont alors recherchées à partir de développements limités[7]^,[8]. Le fait que les matrices soient à diagonale dominante permet diverses approximations de celles-ci[9].

On utilise ci-dessous les fractions molaires ${\displaystyle x_{i}}$, les viscosités ${\displaystyle \eta _{i}}$, la pression ${\displaystyle p}$, la température ${\displaystyle T}$, les masses molaires ${\displaystyle M_{i}}$, les coefficients de diffusion binaires ${\displaystyle {\mathcal {D}}_{ij}}$ et un coefficient lié aux intégrales de collision

${\displaystyle A_{ij}^{*}={\frac {\Lambda _{ij}^{2,2}}{\Lambda _{ij}^{1,1}}}}$

qui caractérise les interactions entre molécules. Lorsque l'on utilise un potentiel Lennard-Jones, on a ${\displaystyle 1,05\leq A_{ij}^{*}\leq 1,15}$[6].

• La première approximation a été obtenue par Buddenberg et Wilke[10] en négligeant tous les termes extra-diagonaux.

${\displaystyle \eta \simeq \sum _{i}{\frac {\eta _{i}}{1+\sum _{j\neq i}{\frac {x_{j}}{x_{i}}}\Psi _{ij}}}}$

avec

${\displaystyle \Psi _{ij}=\alpha {\frac {\eta _{i}}{M_{i}}}\Delta _{ij}\,,\quad \Delta _{ij}={\frac {RT}{p{\mathcal {D}}_{ij}}}}$

Le coefficient ${\displaystyle \alpha }$ qui vaut 2 est dans les faits modifié pour coller au mieux aux résultats. Dans les mélanges gazeux choisis par les auteurs de l'approximation la valeur retenue est ${\displaystyle \alpha =1,385}$. Pour l'air on obtient une meilleure précision en prenant ${\displaystyle \alpha =1,45}$[8].

• Brokaw propose un calcul approché des termes extra-diagonaux[11] qui permet d'identifier ${\displaystyle \alpha }$, de l'ordre de 1,3

${\displaystyle \alpha ={\frac {6}{5}}A_{ij}^{*}}$

• Wilke a proposé une simplification[12] permettant de n'utiliser que le coefficients d'auto-diffusion ${\displaystyle {\mathcal {D}}_{ii}}$ à partir d'un potentiel sphères dures et en supposant tous les ${\displaystyle A_{ij}^{*}}$ égaux entre eux.

En fait on montre[8] que le recours à un potentiel simple n'est pas nécessaire et que l'on peut écrire

${\displaystyle \Psi _{ij}=\left({\frac {M_{j}\eta _{i}}{M_{i}\eta _{j}}}\right)^{\frac {1}{2}}}$

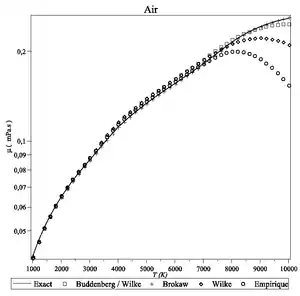
Il existe d'autres approximations plus complexes et plus précises[9]^,[8] mais il faut noter qu'une simple loi de mélange ${\displaystyle \eta =\left(\sum _{i}{\frac {c_{i}}{\eta _{i}}}\right)^{-1}}$, bien que sans justification théorique, donne des résultats très honorables (voir courbe). Dans cette expression, ${\displaystyle c_{i}={\frac {M_{i}x_{i}}{\sum M_{i}x_{i}}}}$ est la fraction massique.

• Portail de la physique
• Portail des sciences des matériaux