Lemme de Newman

En mathématiques et en informatique, plus précisément dans la théorie des relations binaires, le lemme de Newman dit qu'une relation binaire noethérienne est confluente si elle est localement confluente[1]. Une démonstration relativement simple (induction sur une relation bien fondée) est due à Gérard Huet en 1980[2]. La démonstration originale de Newman est plus compliquée, mais la méthode des diagrammes décroissants[Quoi ?] montre bien comment elle fonctionne[3].

Confluence.
Confluence locale.

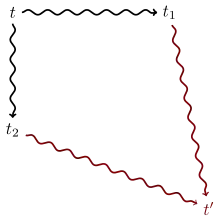
Explication de l'énoncé

Une relation binaire est noethérienne (ou se termine) si toute chaîne d'éléments reliés les uns aux autres par la relation est finie. Elle est localement confluente lorsque si depuis un élément t, on peut aller à t1 par la relation et on peut aussi aller à t2, alors de t1 et de t2 on peut aller par une chaîne de relations à un même élément t'. Elle est confluente lorsque si depuis un élément t, en appliquant une suite de relations on obtient t1, et en appliquant une autre suite de relations on obtient t2, alors t1 et t2 peuvent tous les deux aller vers un même élément t'.

Contre-exemple lorsque la relation binaire n'est pas noethérienne

Considérons la relation binaire suivante → :

  • a → b et b → a
  • a → x
  • b → y

La relation est localement confluente ; par exemple, a → x et a → b et x et b vont tous deux vers x (b → a → x). Par contre, la relation binaire n'est pas confluente : a → x et a → b → y, mais x et y ne peuvent aller vers un même élément (en effet depuis x ou y aucune flèche ne part).

Démonstration
Démonstration du lemme de Newman. On applique la confluence locale (en vert) puis deux fois l'hypothèse d'induction (en orange et brun).

Le lemme de Newman se démontre par induction en utilisant le fait que la relation est noethérienne. Considérons la propriété P(t) : si t → t1, t → t2, alors t1 et t2 vont vers le même élément t'. Si t → t1 en 0 étape (cela signifie t1 = t) ou si t → t2 en 0 étape (cela signifie t2 = t), t1 et t2 vont vers le même élément t'. Les autres cas sont illustrés par la figure de droite.

Applications à la réécriture de termes

Si l'on sait qu'un système de réécriture est noethérien alors la confluence locale est décidable. Ainsi, par le lemme de Newman (et toujours si l'on sait qu'un système de réécriture est noethérien), la confluence est décidable.

Notes
  1. Franz Baader, Tobias Nipkow, (1998) Term Rewriting and All That, Cambridge University Press (ISBN 0-521-77920-0).
  2. Gérard Huet, « Confluent Reductions: Abstract Properties and Applications to Term Rewriting Systems », Journal of the ACM (JACM), October 1980, Volume 27, Issue 4, pp. 797 - 821.
  3. Jan Willem Klop, Vincent van Oostrom, Roel C. de Vrijer, « A geometric proof of confluence by decreasing diagrams », J. Log. Comput. 10(3): 437-460 (2000).

Références
  • M. H. A. Newman (en). On Theories with a Combinatorial Definition of “Equivalence”, Annals of Mathematics, 43, Number 2, pages 223–243, 1942.
  • (en) Michael S. Paterson, Automata, Languages, and Programming : 17th International Colloquium, vol. 443, Warwick University, England, Springer, coll. « Lecture notes in computer science », , 780 p. (ISBN 978-3-540-52826-5, lire en ligne)

Ouvrages
  • Term Rewriting Systems, Terese, Cambridge Tracts in Theoretical Computer Science, 2003. « (livre en ligne) »(Archive • Wikiwix • Archive.is • Google • Que faire ?) (consulté le )
  • Term Rewriting and All That, Franz Baader et Tobias Nipkow, Cambridge University Press, 1998 (livre en ligne)
  • John Harrison, Handbook of Practical Logic and Automated Reasoning, Cambridge University Press, 2009, (ISBN 978-0-521-89957-4), chapitre 4 « Equality ».


  • Portail des mathématiques
  • Portail de la logique
  • Portail de l'informatique théorique
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.