LZ77 et LZ78
LZ77 et LZ78 sont deux algorithmes de compression de données sans perte proposés par Abraham Lempel et Jacob Ziv en 1977 et 1978 (d'où leurs noms). Ces deux algorithmes posent les bases de la plupart des algorithmes de compression par dictionnaire, à tel point qu'on parle couramment d'algorithme LZ pour désigner un algorithme de compression par dictionnaire. Ces algorithmes reposent de manière essentielle sur une mesure de complexité pour les suites de longueur finie, la complexité de Lempel-Ziv.
LZ77
Principe
LZ77 est un algorithme de compression par dictionnaire utilisant une fenêtre glissante ; les motifs déjà rencontrés dans la fenêtre sont remplacés par une référence à leur première apparition (typiquement, par une paire (distance, longueur)).
Par extension, LZ77 est aussi utilisé pour désigner la famille des algorithmes de compression par dictionnaire utilisant une fenêtre glissante, comme LZSS et LZMA.
Compression
Etant donnée une séquence S à compresser, on l'écrit d'abord sous forme de plusieurs composantes Si juxtaposées. Pour ce faire, on choisit un entier LS qui sera la longueur maximale d'un Si et un entier n > LS qui sera la taille du buffer. On initialise les n-Ls caractères du buffer par des zéros et on complète le buffer par les LS premiers caractères de S.
L'entier n-Ls est la taille de la fenêtre glissante (initialisée avec des zéros comme indiqué précédemment). Pour trouver les Si, on réalise à chaque itération une production exhaustive de la sous-séquence de S la plus longue possible en prenant le contenu de la fenêtre glissante comme préfixe, avec ici la contrainte que la longueur de la séquence produite ne peut dépasser Ls.
Après initialisation de la fenêtre à zéro et en appliquant ce processus de production on obtient donc la séquence S1 de longueur L1<Ls puis on fait glisser la fenêtre en enlevant les L1 premiers caractères de la fenêtre glissante du buffer et en faisant entrer dans le buffer les L1 caractères suivants de S. On répète ce procédé (production puis glissement de la fenêtre) pour trouver les autres Si jusqu'à arriver au bout de la séquence S.
Cette décomposition découpe S sous forme de composantes comme dans le processus de calcul de la complexité de Lempel-Ziv.
À chaque étape i, après avoir trouvé Si par un processus de production, on lui affecte un mot de code qui sera sa représentation dans le fichier compressé. Ce mot de code n'est rien d'autre que le triplet (position, longueur, caractère) correspondant.
Chaque Si est ainsi codé par un triplet Ci,1Ci,2Ci,3 et sera représenté ainsi dans le fichier compressé. Le mode de représentation est donc le suivant :
- Ci,1 est la représentation en base α(α étant la taille de l'alphabet des caractères de S) de pi-1, avec pi l'indice dans la fenêtre glissante où commence la copie qui correspond à Si (pi est le pointeur pour la production de Si).
- Ci,2 est la représentation en base α de Li - 1 (la longueur de la production à cette étape)
- Ci,3 est le dernier caractère de Si
Cet algorithme est étroitement lié au calcul de complexité de Lempel-Ziv. Après avoir fait précédé S de n-LS zéros, on ne fait en effet que décomposer S en composantes Si (qu'on remplace par leur mot de code) en prenant, à chaque étape, le contenu de la fenêtre glissante comme préfixe et en ayant une longueur maximale LS fixée pour toutes les composantes.
Vu que pi est un indice appartenant au préfixe (ici, la fenêtre glissante), il est compris entre 1 et n-LS et peut être représenté en base α par α (n-LS) caractères. De même, les Li étant bornés par LS, on a besoin de α (LS) caractères pour représenter Li-1. Ci,3 étant un caractère unique, chaque Si sera représenté dans le fichier compressé par LC = α (n-LS)+ α (LS) + 1 caractères.
Décompression
La décompression est très semblable à la compression.
Initialisation :
- on utilise une fenêtre de taille n-LS qui est initialisée avec des zéros,
- on récupère pi - 1 (et donc pi) sur les α (n-LS) premiers caractères de Ci (Ci,1),
- les α (LS) caractères suivants (Ci,2) donnent la valeur de Li - 1.
Après l'initialisation, à chaque étape i on répète Li -1 fois le processus suivant :
- on recopie le caractère qui est à l'indice pi à la fin de la fenêtre,
- puis on fait glisser la fenêtre vers la droite pour faire sortir son premier caractère et faire entrer le caractère qui vient d'être recopié dans la fenêtre.
Vu que les Li - 1 premiers caractères de Si sont juste une copie de la partie de la fenêtre commençant à l'indice pi, on récupère par le processus ci-dessus les Li -1 premiers caractères de Si. À ce stade, il ne nous manque que le dernier caractère de Si qui n'est rien d'autre que le dernier caractère (Ci,3) de Ci.
Ceci amène à la dernière phase de l'étape i qui consiste à :
- recopier le dernier caractère de Ci (qui est le dernier caractère de Si) à la fin de la fenêtre avant d'effectuer un dernier décalage à droite, d'un caractère, de la fenêtre.
On obtient ainsi Si en récupérant les Li derniers caractères de la fenêtre. Après avoir appliqué ce processus à tous les mots de code Ci, la séquence S est obtenue en concaténant les Si.
Exemple
On applique l'algorithme de compression à la séquence ternaire
S = 001010210210212021021200
dont l'alphabet A={0,1,2} compte α=3 caractères.
On prend n=18 et LS=9.
On commence par calculer LC qui est égale à 5 (n-LS=9 et ).

Compression:
Étape 0. Initialisation du buffer :
On a, dans le buffer de taille n=18, comme expliqué précédemment n-LS=9 zéros suivis des LS=9 premiers caractères de S (cf. Image1).
Étape 1.
Dans cet exemple, n'importe quel indice de la fenêtre glissante pourrait être pris comme p1 (la plus longue correspondance est 00 quel que soit le pointeur initial), on choisit p1 =9 (cf. Image2_lz77)

On obtient donc S1=001; L1=3, ce qui donne :
- C1,1=22 (représentation en base 3 de p1-1 avec 3 (18 - 9)= 2 caractères)
- C1,2=02 (représentation en base 3 de L1 - 1 avec 3 (9)= 2 caractères)
- C1,3=1 (le dernier caractère de S1)
On fait ensuite glisser la fenêtre pour en faire sortir les L1=3 premiers caractères et faire entrer les 3 prochains caractères de S dans le buffer (cf. Image3_lz77).
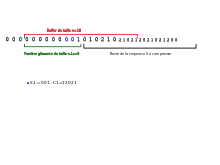
Étape 2.
On passe alors au calcul de C2 (code correspondant à S2) : On prend p2=8 (qui permet d'avoir la plus longue correspondance) avec L2= 4 et S2=0102. En procédant de la même manière que pour S1, on obtient C2=21102 (cf. Image4_lz77 ).

On continue ainsi jusqu'à la fin de la séquence pour trouver C3=20212 et C4=02220.
Après compression, on obtient pour S la séquence compressée :
22021 21102 20212 02220
Décompression:
On procède à la décompression de S comme suit :
- on décompresse dans l'ordre les Ci pour obtenir les Si
- on concatène ces Si pour obtenir S.
Pour C1=22021, on a :
- p1=9 (C1,1=22, les 2 premiers caractères de C1, représente 8 en base 3, d'où p1=8+1=9),
- L1=3 (C1,2=02, les 2 caractères suivants de C1, représente 2 en base 3, d'où L1=2+1=3),
- le dernier caractère C1,3=1 de C1 est le dernier caractère du mot S1.
On applique le processus de décompression présenté ci-dessus à C1 (cf. décompression_lz77). On retrouve ainsi S1=001.
On procède de même, dans l'ordre, pour les Ci qui restent.

Limites et utilisations
LZ77 présente certains défauts, en particulier, si aucune chaîne n'est trouvée dans le dictionnaire, le symbole à compresser est alors codé par "position=0", "longueur=0", "nouveau symbole", c'est-à-dire qu'il occupe 3 octets au lieu d'un seul dans le fichier original. Ce défaut est supprimé dans la variante LZSS.
L'algorithme LZ77 est notamment utilisé dans l'algorithme deflate (avant un codage de Huffman) et pour la compression des fichiers dans le système de fichier Windows NTFS[1].
LZ78
LZ78 est un algorithme de compression par dictionnaire (publié dans (en) « Compression of Individual Sequences via Variable-Rate Coding », IEEE Transactions on Information Theory, ) utilisant un dictionnaire global (et non plus une fenêtre), construit de la même façon par le compresseur et le décompresseur, respectivement à la compression et à la décompression. Cela permet d'éviter le principal problème de son prédécesseur (LZ77) qui ne peut retrouver une chaîne de caractères si elle se trouve en dehors de la fenêtre.
Par extension, LZ78 est aussi utilisé pour désigner la famille des algorithmes de compression par dictionnaire utilisant un dictionnaire implicite, comme Lempel-Ziv-Welch.
LZ78 a eu moins de succès que LZ77, pour des raisons d'efficacité, et parce qu'il a été protégé par un brevet logiciel aux États-Unis.
Voir aussi
- compress : un programme qui utilise l'algorithme Lempel-Ziv-Welch.