Jeu de la vie
Le jeu de la vie est un automate cellulaire imaginé par John Horton Conway en 1970 et qui est probablement le plus connu de tous les automates cellulaires. Malgré des règles très simples, le jeu de la vie est Turing-complet.
Pour les articles homonymes, voir Jeu de la vie (homonymie).
Le jeu de la vie est un jeu de simulation au sens mathématique plutôt que ludique. Bien que n'étant pas décrit par la théorie des jeux, certains le décrivent comme un « jeu à zéro joueur ».
Règles
Le jeu de la vie est un « jeu à zéro joueur », puisqu'il ne nécessite pas l'intervention du joueur lors de son déroulement. Il s’agit d’un automate cellulaire, un modèle où chaque état conduit mécaniquement à l’état suivant à partir de règles pré-établies.
Le jeu se déroule sur une grille à deux dimensions, théoriquement infinie (mais de longueur et de largeur finies et plus ou moins grandes dans la pratique), dont les cases — qu’on appelle des « cellules », par analogie avec les cellules vivantes — peuvent prendre deux états distincts : « vivante » ou « morte ».
Une cellule possède huit voisins, qui sont les cellules adjacentes horizontalement, verticalement et diagonalement.
À chaque étape, l’évolution d’une cellule est entièrement déterminée par l’état de ses huit voisines de la façon suivante :

- une cellule morte possédant exactement trois voisines vivantes devient vivante (elle naît) ;
- une cellule vivante possédant deux ou trois voisines vivantes le reste, sinon elle meurt.
Ainsi, la configuration  donne au tour suivant la configuration
donne au tour suivant la configuration 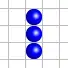 qui redonne ensuite la première.
qui redonne ensuite la première.
On peut également formuler cette évolution ainsi :

- si une cellule a exactement trois voisines vivantes, elle est vivante à l’étape suivante.
- C’est le cas de la cellule verte dans la configuration de gauche ;

- si une cellule a exactement deux voisines vivantes, elle reste dans son état actuel à l’étape suivante.
- Dans le cas de la configuration de gauche, la cellule située entre les deux cellules vivantes reste morte à l’étape suivante ;

- si une cellule a strictement moins de deux ou strictement plus de trois voisines vivantes, elle est morte à l’étape suivante.
- C’est le cas de la cellule rouge dans la configuration de gauche.
L'état suivant d'une cellule est : (S = 3) OU (E = 1 ET S = 2).
Avec :
- S : nombre actuel de cellules vivantes dans son voisinage (entier naturel compris entre 0 et 8 inclus) ;
- E : état actuel de la cellule (entier naturel égal à 0 pour une cellule morte et égal à 1 pour une cellule vivante).
Légende des schémas
Afin de représenter le processus, les cellules vivantes sont généralement représentées colorées sur la grille, sur un fond de cellules mortes incolores.
Les schémas de cet article suivent les conventions de couleur suivantes :
- bleu : cellules en cours de vie
- vert : cellules naissantes
- rouge : cellules mourantes
- jaune : cellules ne vivant qu’une seule génération
Histoire
Le jeu de la vie est inventé par John Horton Conway en 1970, alors qu’il est professeur de mathématiques à l’université de Cambridge, au Royaume-Uni.
J. H. Conway s’intéresse alors à un problème proposé par le mathématicien John Leech dans le domaine de la théorie des groupes et qui avait trait à l’empilement dense de sphères à 24 dimensions (connu comme le réseau de Leech). Il découvre quelques propriétés remarquables et publie les résultats de son étude en 1968. Conway est également intéressé par un problème présenté vers les années 1940 par un mathématicien renommé : John von Neumann.
Ce dernier a essayé de trouver une hypothétique machine qui pourrait s’auto-reproduire. Il y parvient en construisant un modèle mathématique aux règles complexes sur un repère cartésien. Conway essaye de simplifier les idées de von Neumann et finit par réussir. Couplant ses succès précédents avec les réseaux de Leech avec ses travaux sur les machines auto-réplicantes, il donne naissance au jeu de la vie.
Le premier contact entre le grand public et ces travaux se fait en 1970 à travers une publication dans Scientific American dans la rubrique de Martin Gardner : « Mathematical Games »[1].
Gardner écrit dans ses colonnes que « le jeu de la vie rendit Conway rapidement célèbre et il ouvrit aussi un nouveau champ de recherche mathématique, celui des automates cellulaires. En effet, les analogies du jeu de la vie avec le développement, le déclin et les altérations d’une colonie de micro-organismes, le rapprochent des jeux de simulation qui miment les processus de la vie réelle. »
D’après Gardner, Conway expérimenta plusieurs jeux de règles concernant la naissance, la mort et la survie d’une cellule avant d’en choisir un où la population des cellules n’explose pas (ce qui arrive souvent lorsque les conditions de naissances sont moins strictes) mais où des structures intéressantes apparaissent cependant facilement. À l’origine, John Conway y jouait à la main, en utilisant un plateau de go pour grille et des pierres de go pour matérialiser les cellules vivantes.
Plusieurs structures intéressantes furent découvertes, comme le « planeur », un motif qui se décale en diagonale toutes les 4 générations, ou divers « canons » qui génèrent un flux sans fin de planeurs. Ces possibilités augmentent l’intérêt pour le jeu de la vie. De plus sa popularité augmente d’autant qu'il arrive à une époque où une nouvelle génération de mini-ordinateurs meilleur marché est commercialisée, ce qui permet de tester des structures pendant la nuit, lorsque personne d’autre ne les utilise.
Vers la fin des années 1980, la puissance des ordinateurs est suffisante pour permettre la création de programmes de recherche de structures automatiques efficaces ; couplés au développement massif d’Internet, ils conduisent à un renouveau dans la production de structures intéressantes.
Au bout du compte, le jeu de la vie attire plus l’intérêt du grand public sur les automates cellulaires (entre autres grâce à divers économiseurs d’écran) que, par exemple, tous les travaux de Edgar Frank Codd, spécialiste reconnu du domaine et auteur de l’ouvrage de référence Cellular automata (1968)[2].
Structures
Des structures, constituées de plusieurs cellules, peuvent apparaître dans l’univers ; les plus classiques sont :
- les structures stables ;
- les structures périodiques, ou oscillateurs ;
- les vaisseaux ;
- les mathusalems.
Il existe également d’autres structures, qui apparaissent beaucoup plus rarement (voire pas du tout pour les jardins d'éden) dans l’univers de jeu :

- les puffeurs ;
- les canons ;
- les jardins d’Éden ;
- les spacefillers.
Structures stables

Les structures stables (en anglais still life) sont des ensembles de cellules ayant stoppé toute évolution : elles sont dans un état stationnaire et n’évoluent plus tant qu’aucun élément perturbateur n’apparaît dans leur voisinage. Un bloc de quatre cellules est la plus petite structure stable possible.
Certaines figures se stabilisent en structures florales après une succession d'itérations comparables à une floraison.
Oscillateurs

Les oscillateurs se transforment de manière cyclique, en revêtant plusieurs formes différentes avant de retrouver leur état initial. Des figures de ce type sont très nombreuses : on en connaît actuellement des centaines[3]. La « grenouille » est une structure qui se répète toutes les deux générations.
Elles peuvent apparaître relativement facilement dans l’univers de jeu par l’évolution spontanée de « graines » beaucoup plus simples.
Vaisseaux
Les vaisseaux — ou navires — (en anglais spaceships, « vaisseaux spatiaux ») sont des structures capables, après un certain nombre de générations, de produire une copie d’elles-mêmes, mais décalée dans l’univers du jeu.
Le déplacement d’un vaisseau qui retrouve après n étapes sa configuration initiale déplacée de A cases horizontalement et de B cases verticalement est noté A-B, et sa vitesse (A, B)c/n, où c représente la « vitesse de la lumière » dans le jeu de la vie, c'est-à-dire la vitesse maximale d'une cellule par génération. L’existence de vaisseaux de type A - B pour A et B quelconques a été démontrée[réf. souhaitée]. On distingue :
- des vaisseaux de type transversal (ou orthogonaux), c’est-à-dire A = 0 ou B = 0 ;
- des vaisseaux de type diagonal, avec A = ± B ;
- des vaisseaux ayant un déplacement oblique, c'est-à-dire A ≠ ± B. On parle aussi de vaisseau-cavalier (knightship en anglais).
Le premier vaisseau oblique, appelé Gemini, a été découvert par Andrew J. Wade en 2010[4]. Il se déplace de 5 120 cellules verticalement et de 1 024 cellules horizontalement toutes les 33 699 586 générations. Des variantes existent où sa vitesse et sa période sont différentes. C'est aussi un constructeur universel.
On prouve également qu’un vaisseau de type A - B a nécessairement une période N ≥ 2(A+B)[5], donc que la vitesse maximale pour un vaisseau diagonal est (1, 1)c/4, et que celle pour un vaisseau orthogonal est (2, 2)c/4 = (1, 1)c/2.
On sait construire des vaisseaux de taille et de période aussi grandes que souhaitées, en utilisant des séries de composants.[réf. souhaitée]. Le planeur est le plus petit vaisseau du jeu de la vie, qui possède aussi la plus grande vitesse pour un vaisseau diagonal.
Mathusalems
Les mathusalems sont des structures actives qui mettent un certain temps avant de se stabiliser. Certains, comme les « lapins », mettent plus de 15 000 générations avant de se stabiliser en un nombre plus ou moins important de débris variés.
Puffeurs
Les puffeurs (de l’anglais puffer, « générateur de fumée ») sont des configurations qui se déplacent en laissant derrière elles une traînée constituée de débris.
Canons

Les canons, ou lanceurs, ou encore lances-navires (en anglais guns) sont en quelque sorte des oscillateurs lâchant des débris, capables de produire des vaisseaux, à un rythme variable (toutes les 15, 23, 30 ou 360 générations par exemple, ou bien de manière apparemment imprévisible pour les lance-navires pseudo-aléatoires[précision nécessaire]).
De telles structures peuvent être créées à partir de puffeurs que l’on modifie afin que les débris s’agencent sous forme de navires. Le premier canon à avoir été découvert émet un planeur toutes les 30 générations.
Jardins d’Éden

Un jardin d’Éden est une configuration sans passé possible : aucune configuration ne donne à l’étape suivante un jardin d’Éden.
La démonstration mathématique se fonde sur la combinatoire et se trouve notamment dans Winning Ways for your Mathematical Plays, livre publié en 1982 par Berlekamp, Conway, et Guy.
Constructeurs universels
En 2010, Gemini, le tout premier constructeur universel du jeu de la vie, a été découvert. Cette immense figure fait 4 217 807 cellules sur 4 220 191. En avançant, cette figure crée une copie d'elle-même en détruisant la précédente. L'opération prend environ 34 millions de générations. Comme Gemini se déplace et ne laisse rien derrière lui, c'est aussi un vaisseau. C'est d'ailleurs le premier vaisseau à se déplacer obliquement, c'est-à-dire ni orthogonalement, ni diagonalement.
Dimension et complexité

La puissance et la capacité mémoire des ordinateurs personnels depuis le passage au 64 bits permet l’exploration de très grands espaces cellulaires du jeu de la vie. On peut alors en espérer l’émergence de structures complexes d’un haut niveau d’auto-organisation, voire d’esthétique. Stephen Wolfram et d’autres[6] ,[7] ont exploré cette voie. Dès les années 1980, le clown émerge à l’itération 110 d’une dynamique d’un réseau amorcé à partir d’un U initial de 7 cellules (appelé généralement "pi heptomino") formant une image de la lettre U.
N.b. : le clown est formé à l’envers. Pour voir un clown comme sur l’illustration, c’est un U inversé qu’il faut dessiner.
Détails sur la dynamique du réseau : ce « U » de 7 cellules (également appelé heptomino pi) évolue vers une structure complexe et « organique » en passant par des formes très esthétiques. De plus, la structure est auto-reproductible avec un déphasage, la nouvelle structure fille (itération 45) interférant avec une version de la structure mère (itération 15) en cours d’évolution. À l’itération 110 on obtient cette image de « clown ». Puis le réseau se stabilise sur une forme stable oscillante complexe[8].
Questions mathématiques
Certaines propriétés du jeu de la vie ont pu être démontrées, en particulier :
- La croissance d’une configuration est au maximum en t². Cette propriété est triviale pour tout automate cellulaire bi-dimensionnel : dans le cas du jeu de la vie, comme la vitesse de transmission de l'information est de une case par pas de temps dans chacune des 8 directions, le nombre de cellules vivantes est trivialement limité par une borne en 8t². La question serait plutôt de savoir quelle est la configuration dont le taux de croissance est maximal.
- L’existence de portes logiques ET, OU, NON[9]. Ces portes logiques permettent de coder une machine de Turing universelle au sein du jeu de la vie. Par conséquent, le problème qui consiste à prédire le comportement asymptotique de toute structure du jeu de la vie est indécidable.
Calculabilité
Malgré sa simplicité, ce jeu est une machine de Turing universelle : il est possible de calculer tout algorithme pourvu que la grille soit suffisamment grande et les conditions initiales correctes.
Simulation
Plusieurs programmes informatiques simulent le jeu de la vie; dont Mirek's Cellebration[10]. Ceux qui sont écrits en Java ou JavaScript peuvent être inclus facilement dans une page web. Ces simulateurs sont cependant peu efficaces quand ils représentent le terrain par un tableau bi-dimensionnel et se contentent de faire évoluer les cellules en suivant les règles de Conway.
En 1980, Bill Gosper a inventé puis écrit Hashlife, un algorithme de simulation beaucoup plus efficace, permettant de manipuler plusieurs millions de cellules sur des millions de générations en des temps plus courts. Cet algorithme reposait sur une idée différente : en effet, si l’on considère une portion de l’espace du jeu relativement isolée de ses voisines, il est possible de la faire « tourner » pendant un certain nombre n de générations, puis de mémoriser le résultat. Si la configuration de départ se reproduit ailleurs, on pourra alors « sauter » directement n générations pour cette partie du jeu. Ce nouvel algorithme faisait donc « tourner » différentes portions de l’espace à des vitesses différentes et parvenait à préserver la cohérence aux bordures de chaque région ainsi simulée. Il faisait appel à une table de hachage pour mémoriser et retrouver rapidement des configurations locales.
Le jeu de la vie est extrêmement sensible à la manière de calculer la génération suivante. L'implémentation classique est synchrone, c'est-à-dire que l'état de chaque cellule de génération n+1 est calculé à partir de l'état des cellules de génération n. Bersini et Detours ont montré que les comportements intéressants du jeu de la vie disparaissent avec la quasi-totalité des schémas de mise à jours non synchrones (où les états n+1 peuvent s'influencer les uns les autres, comme dans la vraie vie)[11]. Cependant, Nehaniv a montré que tout comportement synchrone peut être émulé par des automates cellulaires asynchrones et il est donc possible de retrouver le comportement du jeu de la vie sans « horloge globale » cadençant l'évolution des générations[12],[13].
Depuis 2008, de nombreux programmes (dont le plus connu est Golly[14]) intègrent cet algorithme dans une interface graphique. Ils ont permis de créer des configurations énormes et très ingénieuses et de suivre leur évolution, insufflant une nouvelle dynamique dans l’étude déjà très riche de cet automate cellulaire.
Depuis 2012, une recherche sur Google des termes « Conway's game of life » fait apparaître un easter-egg : un jeu de la vie interactif s'affiche en arrière-plan[15].
Variantes
Il existe des variantes du jeu de la vie, fondées sur des règles de voisinage légèrement différentes, par exemple HighLife ou Day & night. Cette variante comporte deux types de cellules, les « positives » et les « négatives », chacune répondant aux mêmes règles, à la différence du signe. Une cellule positive nécessite une somme de 3 pour « naître », une négative une somme de −3. Les cellules vivantes s’intègrent dans le bilan des cellules alentour pour leur survie ou leur déclin. Les deux populations ne peuvent en général survivre côte à côte.
Bibliographie
![]() : document utilisé comme source pour la rédaction de cet article.
: document utilisé comme source pour la rédaction de cet article.
- (en) Martin Gardner, « Mathematical Games. The fantastic combinations of John Conway’s new solitaire game « life », Scientific American, no 223, , p. 120-123 (lire en ligne, consulté le )

- (en) Edgar Frank Codd, Cellular Automata, New York Academic Press,

- Jean-Paul Delahaye, Jeux finis et infinis, Éditions du Seuil, (ISBN 978-2-02-096483-8), chap. 1 (« Quarante ans de jeu de la vie »)
Notes et références
Notes
Références
- (Gardner 1970).
- (Codd 1968).
- (en) « Liste d'oscillateurs », sur LifeWiki
- (en)Adam P. Goucher, Oblique Life spaceship created, Game of Life News, 19 mai 2010, (consulté le 11 mai 2010).
- Thomas Morin, « Vitesse limite des vaisseaux : démonstration », (consulté le ).
- Bernard Feltz et al, Emergence and Reductionism: from the Game of Life to Science of Life, in SELF-ORGANIZATION AND EMERGENCE IN LIFE SCIENCES, Springer Netherlands Editor, 2006, (ISBN 978-1-4020-3916-4) (Print) 978-1-4020-3917-1 (Online)
- N. M. Gotts, Emergent phenomena in large sparse random arrays of Conway’s Game of Life, in INTERNATIONAL JOURNAL ON SYSTEM SCIENCES, Volume 31, Issue 7 July 2000, pages 873 - 894
- Jean-Claude Perez, « DE NOUVELLES VOIES VERS L’INTELLIGENCE ARTIFICIELLE : pluri-disciplinarité, auto-organisation et réseaux neuronaux », 1988, Éd. Masson Paris(ré-édition en 1989), pages 261-262, (ISBN 2-225-81815-0).
- E. R. Berlekamp, J. H. Conway, R. K. Guy, Winning Ways for Your Mathematical Plays, A K Peters/CRC Press; 2nd edition (March 30, 2004)
- (en) « Mirek's Cellebration Download Area », sur mirekw.com (consulté le ).
- H. Bersini, V. Detours, « Asynchrony Induces Stability in Cellular Automata Based Models », In Proceedings of the IVth Conference on Artificial Life - MIT Press/Bradford Books, 1994.
- C. L. Nehaniv, « Evolution in Asynchronous Cellular Automata », Artificial Life VIII, 65-73, MIT Press, 2002.
- C. L. Nehaniv, « Asynchronous Automata Networks Can Emulate Any Synchronous Automata Network », International Journal of Algebra & Computation, 14(5-6):719-739, 2004.
- Golly sur SourceForge.net.
- en:List of Google's hoaxes and easter eggs#Search
Voir aussi
Articles connexes
Liens externes
- Jean-Paul Delahaye, « Le royaume du Jeu de la vie » [PDF], Pour la Science - n° 378,
- (en) Golly, un logiciel de simulation du jeu de la vie
- (en) Site communautaire ConwayLife.com
- (en) Conway's Game of Life: A pop-up Java applet that displays a collection of the greatest patterns ever created in Conway's Game of Life.
- Portail de l’informatique
- Portail de l'informatique théorique