Isostasie

En géologie, l’isostasie, appelée aussi équilibre isostatique, est un phénomène par lequel les éléments de la croûte terrestre ou, plus généralement, de la lithosphère qui se trouvent enfouis à de faibles profondeurs (de l'ordre de 100 km) sont soumis à la même pression indépendamment des irrégularités topographiques en surface. Ce modèle postule en effet qu'un excès de masse en surface tel que les montagnes est compensé par un déficit de masse en profondeur. Il explique l'équilibre de la lithosphère rigide sur l'asthénosphère ductile. La compensation isostatique contrecarre l'érosion. C'est ainsi que la roche plutonique est mise au jour.

Ne doit pas être confondu avec Eustatisme.

Description du concept

Son origine

Le concept d'isostasie a été formulé par des géodésiens afin d'expliquer leurs observations qui indiquaient que les chaînes de montagnes exercent sur un fil à plomb ou sur un gravimètre une attraction moindre que celle à laquelle on devrait s'attendre compte tenu de la masse des montagnes[note 1]. Il se base sur l'hypothèse que même en terrain fort accidenté, il existe en profondeur une surface de compensation sur laquelle les tensions se réduisent à une simple pression hydrostatique (ou mieux, dans ce contexte : pression lithostatique) s'exerçant normalement partout sur la surface de compensation. Si le concept existait depuis longtemps, le nom « isostasie » ne fut proposé qu'en 1889 par le géologue américain Clarence Edward Dutton (1841–1912). Ce néologisme est dérivé du mot grec isostasios, de iso (égal) et statikos (stable) : il signifie en gros « même équilibre stable partout ». Dutton note qu'il aurait préféré utiliser le terme « isobarie » (égale pression), mais il était déjà utilisé dans un autre contexte. « Équilibre isostatique » signifie que les éléments de la croûte ou, plus généralement, de la lithosphère qui se trouvent enfouis à des profondeurs pas trop grandes (de l'ordre de 100 km, par exemple) sont soumis à la même pression indépendamment des irrégularités topographiques en surface. La profondeur à laquelle l'équilibre isostatique est atteint s'appelle « profondeur de compensation ». Cette dernière peut varier d'un endroit à l'autre.

Son principe

Si toutes les masses topographiques sont compensées, on dit que l'équilibre isostatique est complet. Si seulement une partie des masses topographiques est compensée, on parle de « sous-compensation » ; dans le cas contraire, c'est-à-dire si l'effet des masses compensatoires introduites dans les calculs isostatiques dépassent l'effet des masses topographiques, on parle de « surcompensation ». En outre, on distingue l'« isostasie locale » de l'« isostasie régionale » : dans le premier cas, des parties du relief aussi petites que l'on veut se trouvent compensées par la distribution des masses en profondeur, tandis que dans le deuxième cas, seul des blocs appréciables, de 50 ou 100 kilomètres de diamètre, sont compensés isostatiquement, mais des éléments de ces blocs peuvent être en non-équilibre[1].

L'isostasie désigne un état statique, et non un phénomène de rééquilibrage dynamique de l'altitude de la croûte continentale par rapport au géoïde, comme il est souvent dit. La manière dont l'équilibre isostatique est atteint n'a pas d'importance dans les calculs géodésiques, comme nous le verrons plus loin. Il est hautement dommageable pour la précision du vocabulaire scientifique que de nombreux géologues et tectoniciens utilisent au XXIe siècle des termes comme « soulèvement isostatique » ou « rebond isostatique ». En outre, l'analogie répétée ad infinitum qu'un morceau de lithosphère en équilibre isostatique est comparable à un iceberg flottant dans la mer sous l'action de la poussée d'Archimède qui équilibre la pesanteur est pour le moins simpliste, et le plus souvent ne rend pas compte de manière correcte de la façon dont l'équilibre isostatique est atteint. Cette image d'un iceberg en flottaison est suggérée par l'hypothèse d'Airy exposée plus loin, mais fait peu de cas des forces internes qui sont en présence dans la lithosphère, l'asthénosphère, et les parties plus profondes du manteau terrestre. D'autre part, la façon dont Airy décrit l'état isostatique n'est qu'une possibilité parmi d'autres : sa validité n'est pas universelle. Néanmoins, la surface de contact entre la base de l'iceberg et l'eau de mer donne une idée exacte d'une surface de compensation.

Historique du concept d'isostasie

Le premier qui semble avoir eu confusément l'idée de ce qu'est l'isostasie, fut probablement Léonard de Vinci (1452–1519)[2]. Son raisonnement s'inscrit encore dans le cadre du système géocentrique de Ptolémée, mais stipule que la densité des montagnes est inférieure à celle des terres plus basses. Cette idée rejoint le modèle d'isostasie « à la Pratt » exposé ci-dessous.

Environ deux siècles et demi plus tard (en 1749), Pierre Bouguer (1698–1758), membre éminent d'une fameuse expédition envoyée par l'Académie des sciences en Équateur pour y déterminer la longueur d'un degré d'arc de méridien dans le but de clarifier la figure de la Terre, exprime dans un livre[3] la conviction que l'attraction de l'énorme masse des Andes est bien plus faible que celle à laquelle on s'attendrait de la part du volume de matière représenté par ces montagnes[note 2]. Le géodésien britannique George Everest fait la même observation en analysant ses mesures géodésiques obtenues de 1840 à 1859 dans le nord de l'Inde, au pied de l'Himalaya[4].

Entre-temps, Roger Boscovich fournit une explication du phénomène découvert par Bouguer en écrivant[5] : « « Les montagnes, je pense, doivent s'expliquer principalement comme étant dues à la dilatation thermique du matériau en profondeur, ce qui fait remonter les couches rocheuses proches de la surface ; le vide à l'intérieur de la montagne compense pour les masses situées au-dessus ». C'est ici qu'est utilisé pour la première fois le mot « compenser », et le point de vue de Boscovich approche de près l'hypothèse d'isostasie émise plus tard par John Henry Pratt.

Modèles de compensation isostatique

Trois principaux modèles sont proposés[6] :

  • le modèle Airy–Heiskanen (1855) : la couche supérieure rigide et la couche inférieure fluide ont chacune une densité constante, ρu et ρs, respectivement. Ce modèle s'adapte aux chaînes de montagnes dont l'origine est la superposition tectonique de couches de densités presque identiques. Ces reliefs sont donc compensés par une racine crustale, tandis que les dépressions sont compensées par une anti-racine.
  • le modèle Pratt–Hayford (1854) : la profondeur de compensation est constante et forme la base de la couche rigide. Ce modèle s'adapte à la lithosphère océanique dont la densité croît avec l'âge.
  • le modèle Vening Meinesz[7] ou modèle du rebond flexural (1950) : la compensation régionale intègre l'élasticité lithosphérique. Ce modèle s'adapte à la subsidence de vastes domaines (fronts des chaînes de montagne, gouttières autour des îles volcaniques), à la surcharge des calottes glaciaires, aux épaulements de rifts[8].
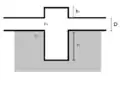  • Modèle Airy-Heiskanen
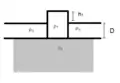  • Modèle Pratt-Hayford
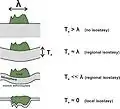  • Modèle Vening Meinesz

Déformations isostatiques

Mécanismes

Ces déformations viennent s'ajouter aux déformations tectoniques régionales ou locales (subsidence ou soulèvement, compression ou déchirement) qui sont directement induites par la tectonique des plaques et d'ampleur souvent faibles, voire négligeables aux échelles humaines de temps[9].
Ces déformations isostatiques sont essentiellement liées aux avancées et recul (et donc aux alourdissement et allègements successifs) des calottes glaciaires.
Ces déformations (glacio-isostasie) sont actuellement plus visibles dans l'hémisphère Nord où les terres émergées sont plus présentes à proximité du pôle. Il semble en outre que les glaces polaires arctiques fondent bien plus vite que celles de l'Antarctique.

Amplitude, intensité, position/extension des déformations isostatiques

Toutes ces dimensions sont liées aux transferts de masse. Ceux-ci s'effectuent essentiellement sous forme de formation et déplacement de glace et/ou d'eaux (les sédiments n'intervenant que peu à ces échelles massiques et spatiotemporelles)[9] ;
Ces déformations seront liées à l'ampleur et à la position des « surcharges »[9] (Cf. masses d'eau ou volumes, poids et surfaces des glaciers). Un autre facteur est la durée de vie, et position géographique de cette masse. Deux autres facteurs sont les spécificités locales de la lithosphère d'une part et du manteau sous-lithosphérique d'autre part (épaisseur élastique, viscosité, rugosité, propriétés rhéologiques...)[9].
Dans chaque hémisphère, deux masses principales (eau et glace) modifient la pression exercée sur la lithosphère. Elles sont toutes deux liées aux températures moyennes et agissent souvent synergiquement (en synergie positive, négative ou équilibrante selon les régions et le moment temporel) ;
Dans notre contexte de déglaciation, ces deux masses donnent deux facteurs de causalité :

    • la fonte des calottes glaciaires (qui allège les pressions portées sur la zone polaire actuelle, et de l'ancienne calotte glaciaire)
    • le poids de la colonne d'eau, liée à la montée de la mer (qui augmente la pression sur le plancher océanique).
Les déformations et mouvements verticaux liés aux déplacements des masses d’eau (hydro-isostasie) peuvent, selon les régions, augmenter ou diminuer ceux de l’isostasie glaciaire[9].
Le dernier grand évènement géologique est la dernière déglaciation (encore en cours et entamée il y a environ 18 000 ans[10]). Il y a 20 000 ans, la mer était 120 mètres plus basse qu'actuellement, et l'Europe était en partie couverte d'une épaisse couche de glace[9].

Modélisation de la déformation isostatique

De nombreux facteurs seraient idéalement à prendre en compte (dont la force de Coriolis, des inerties diverses, l'effet des failles et de la structure du Moho, les effets des « marées terrestres », etc.), mais de manière simplifiée, on peut décomposer les facteurs de déformation en 3 composantes[9] :

  1. une composante liée à la rigidité (« rigidité flexurale » globale, plus ou moins homogène) de la lithosphère ;
  2. une composante « glacioisostatique » ;
  3. une composante « hydroisostatique ».
Pour la période « récente », le long des côtes atlantiques[10], selon les modèles et calculs récents prenant en compte les effets combinés de la tectonique, de l'eustatisme (montée du niveau marin, ici corrigée des effets glacio-hydro-isostatiques), ces composantes isostatiques (de l’ordre du mm/an), expliqueraient à elles seules des différences de niveau qui ont atteint 20 mètres il y a 12 000 ans BP, et 10 mètres il y a 8 000 ans BP. Ainsi, « au sud de la mer du Nord, les marqueurs de niveaux littoraux, mieux préservés dans cette région plus subsidente, confirment l’existence d’un affaissement, de près de 7,5 mètres depuis 8 000 ans, du nord de l’Allemagne par rapport à la Belgique. Il est associé à la poursuite de l’effondrement du bombement frontal périglaciaire. »[9]
Ces modélisations sont utiles pour la prospective (Ces déformations, à croiser avec les tendances locales à la subsidence ou surrection de l’écorce terrestre) sont encore mal connues et comprises, or elles vont localement aggraver ou au contraire limiter la montée perçue (relative) du niveau marin) ; Ces données sont nécessaires pour réévaluer plus finement le risque d'inondation, le risque d'érosion du trait de côte, le risque sismique (en mer notamment, où les installations offshore se sont multipliées depuis les années 1970). Elles permettent aussi de corriger les données des marégraphes (Ex : le Finistère se soulève (par rapport à la Bretagne centrale) ; Brest se soulève de 0,7 mm/an +/- 0,25 ; donnée ne pouvant être « ni régionalisée, ni extrapolées dans le temps »[9]. Il est important de le savoir pour analyser en les contextualisant les données du marégraphe de Brest qui de 1889 à 1962 a enregistré une « élévation relative du niveau marin » de 1,8 mm/an, ce qui porte la variation absolue à 2,5 mm/an si l'on tient compte de la surrection de la croûte terrestre (de 0,7 mm/an) dans cette région (selon les mesures de nivellements)[9].

Convection dans le manteau terrestre et équilibre isostatique

Un équilibre isostatique parfait n'est possible que lorsque le matériau du manteau est au repos. Cependant, la convection thermique est présente dans le manteau. Dans un tel cas, seule l'hypothèse plus générale de DDI (Deep Dynamic Isostasy) peut être satisfaite[11].

Références
  1. Watts A.B.: Isostasy and Flexure of the Lithosphere. Cambridge University Press, 2001, s. 15-17. (ISBN 0-521-00600-7).
  2. John P. Delaney (1940). Leonardo da Vinci on isostasy, Science 91, 546.
  3. Pierre Bouguer (1749). La figure de la Terre, Paris, p. 364.
  4. Vincent Deparis, Hilaire Legros, Voyage à l'intérieur de la terre. De la géographie antique à la géophysique moderne. Une histoire des idées, CNRS Éditions, , p. 311.
  5. Roger Joseph Boscovich (1750). De litteraria expeditione per pontificiam ditionem, p. 450.
  6. Maurice Renard, Yves Lagabrielle, Erwan Martin, Marc de Rafelis Saint Sauveur, Éléments de géologie, Dunod, , p. 221.
  7. F.A. Vening-Meinesz, « Les grabens africains, résultat de compression ou de tension dans la croûte terrestre », Bull. Inst. Rech. Colon. Belg., no 21,‎ , p. 539-552.
  8. (en) C. Ruppel, « Extensional processes in continental lithosphere », Geodesy and Gravity Tectonophysics, vol. 100, no B12,‎ , p. 24187-24215 (10.1029/95JB02955).
  9. BRGM, « Revue du BRGM pour une Terre Durable BRGM's journal for a sustainable Earth »(Archive • Wikiwix • Archive.is • Google • Que faire ?), N° 9 ; avril 2009 - Voir chapitre : Les flux sédimentaires, témoins de l’évolution des reliefs des marges continentales (page 18 et suivantes)
  10. Lambeck K.(1997) Sea-level change along the French Atlantic and Channel Coasts since the time of the Last Glacial Maximum. Paleogeogr. Plaeoclimatol. Paleoecol., 129, 1-22.
  11. Czechowski L., 2019. Mantle flow and determining position of LAB using assumption about isostasy. PAGEOPH, https://link.springer.com/article/10.1007/s00024-019-02093-8

Notes
  1. Dans le cas des mesures au fil à plomb, on parle de déviation de la verticale (ou anomalie de la verticale), dans le cas de mesures de la pesanteur on parle d'anomalie gravimétrique (ou anomalie de la pesanteur).
  2. Au Chimborazo en 1738, Bouguer, après avoir calculé théoriquement la déviation de la verticale à une de ses stations, en fonction de la masse de la montagne et trouvé que la valeur observée était inférieure à la valeur calculée, soupçonna l'existence sous la montagne de cavités ou de masses de densité anormalement faibles. À ce titre, on doit le considérer comme le précurseur des théories modernes de l'isostasie.

Voir aussi

Article connexe

Bibliographie
  • Bonnet s., Guillocheau F., Brun j.P., Van Den Driesche j. (2000) Large-scale relief development related to Quaternary tectonic uplift of a Proterozoic-Paleozoic basement: the Armorican Massif, NW France. Journal of Geophysical Research, 105, B8, 19273-19288.
  • Collina-Girard J. (2002), Underwater mapping of Late Quaternary submerged shorelines in the Western Mediterranean Sea and the Caribbean Sea . Quaternary International, 92, 63-72.
  • Dubois, J. & Diament, M. (1997), Géophysique, Masson, Paris. 205 pp. (ISBN 2-225-83033-9).
  • GIEC (2007) - Bilan 2007 des changements climatiques – Résumé pour les décideurs .
  • Heiskanen, W.A. & Vening Meinesz, F.A.(1958), The Earth and Its Gravity Field, McGraw-Hill, New York. X + 470 pp.
  • Lambeck K. (1997), Sea-level change along the French Atlantic and Channel Coasts since the time of the Last Glacial Maximum . Paleogeogr. Plaeoclimatol. Paleoecol., 129, 1-22.
  • Lambeck K. (1988). Geophysical Geodesy: The Slow Deformations of the Earth, Clarendon Press, Oxford. XII + 718 pp. (ISBN 0-19-854437-5).
  • Lambeck K. et Bard D. (2000), Sea level changes along the French Mediterranean coast from the past 30,000 years ; Earth planet. Sci. Letters, 175, 202-22.
  • Lenôtre, N., Thierry, P., Blanchin, R. & Brochard, G. (1999) Two comparative levelling methods for demonstrating current vertical movements and their application to Brittany (France) . Tectonophysics, 301, p. 333-344
  • Toucanne S. (2008) Reconstruction des transferts sédimentaires en provenance du système glaciaire de mer d’Irlande et du paléo-fleuve Manche au cours des derniers cycles climatiques . Thèse Université de Bordeaux I, 340 p.
  • Vella C., Provansal M. (2000), Relative sea-level rise and neotectonic events during the last 6500 yr on the southern eastern Rhône delta, France . Marine Geology, 170, 27-39.
  • Meinesz FAV (1931) Une nouvelle méthode pour la réduction isostatique régionale de l’intensité de la pesanteur. Bulletin Géodésique (1922-1941), 29(1), 33-51 (extrait / 2 premières pages).
  • Meinesz FV (1939), Tables fondamentales pour la réduction isostatique régionale. Bulletin géodésique, 63(1), 711-776 extrait (2 premières pages)
  • Pirazzoli, P. A. (1997). Mobilité verticale des côtes méditerranéennes à la fin de l'Holocène : une comparaison entre données de terrain et modélisation isostatique. Bulletin de l'Institut océanographique, 15-33 (fiche inist-CNRS).
  • Portail de la géodésie et de la géophysique
  • Portail de la géologie
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.