Inharmonicité
L'inharmonicité définit la nature d'un son musical dont les composantes, que l'on appelle partiels ne sont pas harmoniques, c'est-à-dire ne sont pas à des fréquences multiples entiers du son fondamental.
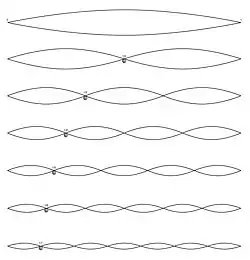
L'harmonicité d'un son indique son absence d'inharmonicité, c’est-à-dire que les fréquences de ses harmoniques sont rigoureusement des multiples entiers du son fondamental, comme dans le modèle mathématique d'un phénomène périodique.
Le vocabulaire des musiciens diffère du vocabulaire des acousticiens. Lorsqu'un musicien joue en harmoniques, il joue pour l'acousticien sur des partiels de la corde ou du tuyau. Le mot partiels n'appartient pas au vocabulaire des musiciens, qui parlent du timbre de façon plus globale sans en disséquer les composantes.
Dans la pratique, inharmonicité ou harmonicité se recoupent par leur relativité, car parler d'un son faiblement inharmonique revient à parler d'un son relativement harmonique... En effet, si le cas du piano et de la cloche sont souvent cités à propos de l'inharmonicité, tous les instruments à sons non entretenus présentent une inharmonicité qui peut être relativement faible, quand il s'agit d'instruments à cordes, ou très importante, dans le cas d'instruments à percussion.
Le cas des instruments à sons entretenus est très différent car un son entretenu est périodique : ses composantes sont harmoniques, à des fréquences effectivement multiples entiers du son fondamental, comme pour tout phénomène périodique. Pour les cordes frottées (famille du violon), ces harmoniques utilisent la résonance des partiels de la corde en les excitant à une fréquence légèrement plus basse que leur fréquence propre (puisqu'il faut corriger leur inharmonicité pour produire la périodicité). Pour un instrument à vent, les fréquences propres du résonateur, que l'on appelle « partiels du tuyau », sont plus ou moins bien accordés sur des valeurs harmoniques selon que l'instrument est construit plus ou moins juste. Lorsqu'un partiel du tuyau est mal accordé, l'harmonique du son excite le résonateur en dehors d'une fréquence de résonance. La conséquence en est l'absence plus ou moins marquée de cette composante dans le son produit. Par exemple, pour une clarinette, il n'y a pas de résonance du tuyau à deux fois la fréquence du fondamental : l'harmonique deux est absent du spectre et, si l'on pousse le son, l'instrument n'« octavie » pas (il « quintoie »).
L'inharmonicité est une caractéristique qui affecte le timbre du son, la hauteur perçue et se vérifie par l'examen de son spectre harmonique. Ce phénomène peut produire plusieurs hauteurs que l'on entend simultanément, comme pour la cloche.
Le piano
L'inharmonicité du piano est due à la raideur de ses cordes. En effet, plus un mode vibratoire de la corde est élevé, plus le nombre de fuseaux est élevé et plus la raideur apporte, par unité de longueur, une force de rappel importante qui s'ajoute à la tension[1]. Cela a pour effet de dilater légèrement la plage des partiels (en comparaison avec des harmoniques).
Cet effet est d'autant plus important que les cordes sont courtes, et donc sera très important dans l'aigu. L'inharmonicité étant variable d'une corde à l'autre, selon son diamètre, sa longueur et sa tension, ceci a pour conséquence qu'il est en général impossible d'obtenir un accord correct entre deux piano très différents. Si on les accorde correctement pour le do central, les deux pianos seront d'autant plus désaccordés qu'ils sont différents.
L'inharmonicité du piano est somme toute faible, en regard de celle des cloches, mais non négligeable. L'accord du piano traite cette inharmonicité par le phénomène d'« écartement » des octaves, afin de retrouver plus de consonance. En effet, l'inharmonicité contracte les intervalles au fur et à mesure que l'on s'élève dans la tessiture du piano. Lorsque les octaves sont accordées parfaitement pures (sans battement), les autres intervalles générés par ce report d'octaves pures deviennent acoustiquement et perceptivement de plus en plus courts. L'agrandissement acoustique des octaves toujours pratiqué par les accordeurs expérimentés compense le phénomène. Un tempérament théorisé découle de cette pratique, le tempérament égal à quintes justes.
La cloche
Dans le cas de la cloche, l'ordre des partiels ne suit pas l'ordre habituel des harmoniques. Le partiel no 1 s'entend très peu. Le partiel no 2 est à l'octave. Le partiel no 3 est, en général, à la tierce mineure, plus rarement à la tierce majeure. Tout l'art du fondeur de cloches consiste donc à réaliser une cloche dont les partiels sont accordés, afin d'obtenir la plus belle sonorité par un accord consonant mineur (ou plus rarement majeur). Certains compositeurs actuels ont utilisé cette disposition d'harmoniques dans leurs œuvres, afin de recréer, par exemple avec un orchestre, une sonorité qui évoque celle de la cloche.
Autres cas
Lorsque le xylophone est utilisé pour initier les enfants au solfège, une deuxième hauteur peut être entendue par l'enfant, qui n'est pas celle de la note annoncée[réf. souhaitée].
Dans le chant diphonique, le signal sonore est périodique, c'est l'un des harmoniques que l'on entend et que l'on suit mélodiquement : le chanteur concentre une énergie acoustique importante sur cette harmonique, qu'il parvient à renforcer indépendamment de ses voisines.
Les instruments à vent peuvent, également, fonctionner en régime multiphonique. Ces techniques sont beaucoup utilisées en musique contemporaine. On entend alors plusieurs hauteurs simultanément.
Dans certains gongs, les partiels sont couplés en sorte que des partiels aigus se renforcent au cours du temps. Le son augmente, au lieu de s'atténuer comme nous en avons l'habitude. Dans ces cas, ce sont des partiels basses fréquences qui fournissent, par des mécanismes non linéaires, l'énergie aux partiels aigus.
Notes
- Contrairement à ce qu'on peut lire dans certains ouvrages peu familiers avec la physique, ce n'est pas aux extrémités de la corde que se situe l'effet principal de raideur, mais tout au long de la corde. Une autre erreur consiste à croire que la raideur serait d'autant plus grande que la corde est plus tendue. C'est exactement l'inverse qui est vrai : la raideur d'une corde contribue d'autant moins que sa tension est grande. Voir formules dans Inharmonicité du piano.
Articles connexes
- Portail de la musique
- Portail de la musique classique
- Portail de la physique
- Portail des sciences