Inégalité de Huygens
L'inégalité de Huygens est un résultat mathématique établissant que, sur l'intervalle de , l'inégalité suivante est vérifiée : .
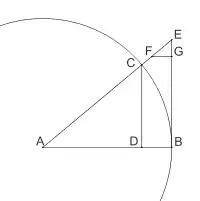
Cette inégalité signifie que, dans le dessin ci-contre, la longueur de l'arc BC est inférieure à la moyenne pondérée de la longueur CD affectée du coefficient 2 et de la longueur BE affectée du coefficient 1, ou, plus simplement, que la longueur de l'arc BC est plus petite que celle du segment [BG].
Démonstration par l'utilisation de la dérivée
Soit f fonction qui à tout x de , associe .
Cette fonction est dérivable sur cet intervalle comme somme de fonctions dérivables.
La fonction dérivée de f est la fonction f' qui à tout x de l'intervalle considéré associe :
- .
Sur l'intervalle considéré, les inégalités suivantes sont vérifiées : et .
Donc, et la fonction f est croissante sur l'intervalle considéré.
On remarque l'égalité : par conséquent :
Note historique
Cette inégalité, associée à cette minoration[1]:
fournit un meilleur encadrement de x que le simple encadrement
Appliqué à , cet encadrement sert à améliorer la méthode d'Archimède pour calculer Pi. En fait, Snell, dans sa Cyclometria (1621) énonçait déjà cette formule, mais sans la démontrer rigoureusement[2]. Huygens dans son ouvrage de Circuli dimensione (1654) se propose de démontrer ces inégalités et d'en présenter d'autres, utiles à la quadrature du cercle approchée[3]. Ce problème ancien, déjà abordé par Nicolas de Cuse dans son De mathematica perfectione (1512), avait fait l'objet plus récemment d'un travail de Grégoire de Saint-Vincent, Opus geometricum quadraturae circuli (1647).
La démonstration de Huygens diffère de celle indiquée ci-dessus : elle est géométrique. Bien que Huygens dans des travaux ultérieurs sur la cycloïde détermine les tangentes de diverses courbes, il restera toujours prudent vis-à-vis du calculus.
La démonstration que l'on peut tirer du de Circuli[4], est assez astucieuse et se réfère, d'une part à une inégalité d'aires, itérée, d'autre part à des propriétés de proportionnalités entre segments.
Il existe de nos jours des dizaines d'inégalités de ce type[5] démontrées maintenant avec des outils d'analyse (Développement limité, règle de l'Hôpital sur la monotonie,...)
Notes et références
- Christian Huygens, De circuli magnitudine inventa, Théorème VII Proposition VII, Œuvres complètes de Christiaan Huygens. Travaux de mathématiques pures, 1652-1656 / publ. par la Société hollandaise des sciences, p 132
- Cf. « Œuvres complètes de Christiaan Huygens. Travaux de mathématiques pures, 1652-1656 », Société hollandaise des sciences, p. 95
- Huygens craint en particulier de se faire devancer par Marcus Marci (Œuvres complètes de Christiaan Huygens. Travaux de mathématiques pures, 1652-1656 / publ. par la Société hollandaise des sciences, p. 98)
- Christian Huygens, De circuli magnitudine inventa, théorèmes IV, VI, VIII et IX
- Voir par exemple Some new inequalities of the Huygens type, Ling Zhu, 2009,ou encore The natural approach of wilker-cusa-huygens inequalities, Cristinel Mortici, 2010
Voir aussi
Articles connexes
Bibliographie
- Œuvres complètes de Christiaan Huygens. Travaux de mathématiques pures, 1652-1656 / publ. par la Société hollandaise des sciences - 1888/1950- Bibliothèque nationale de France, 4-R-788 (12)
- Portail de l'analyse