Hydrogéologie
L'hydrogéologie (de hydro-, eau et géologie, étude de la terre), également nommée hydrologie souterraine et plus rarement géohydrologie, est la science qui étudie l'eau souterraine. Son domaine d'étude repose essentiellement sur deux branches des sciences de la Terre, la géologie et l'hydrologie, mais aussi sur de nombreuses autres branches comme la géostatistique, la physique, la chimie, la biologie, la géochimie, l'hydrochimie, la géophysique, l'hydrodynamique, l'hydraulique souterraine, l'analyse numérique ainsi que des techniques de modélisation. À ce titre, l'hydrogéologie est par excellence une science interdisciplinaire.
« Géohydrologie » redirige ici. Ne pas confondre avec Géodrilologie, la science des vers de terre.
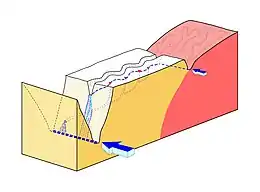
L'hydrogéologie s'occupe de la distribution et de la circulation de l'eau souterraine dans le sol et les roches, en tenant compte de leurs interactions avec les conditions géologiques et l'eau de surface.
L'hydrogéologie par rapport à d'autres branches

L'hydrogéologie comme la plupart des sciences de la Terre est une branche interdisciplinaire. Bien que les principes de base de l'hydrogéologie soient intuitifs (par exemple, l'eau coule vers le bas), l'étude de leurs interactions peut être très complexe. De façon générale, le fait de prendre en compte les interactions de différentes facettes d'un système à plusieurs composantes demande une connaissance de plusieurs branches tant au niveau expérimental que théorique.
L'hydrogéologie est une branche des sciences de la Terre qui s'occupe du flux de l'eau souterraine à travers les aquifères et autres milieux poreux peu profonds (généralement moins 1 000 mètres sous la surface). Le flux de l'eau très peu profonde (plus haute que 3 mètres sous la surface) est une branche pertinente pour la pédologie, l'agriculture et le génie civil, autant que pour l'hydrologie. Le flux de fluides que l'on trouve dans des formations plus profondes (tels que l'eau mais aussi les hydrates de carbone et les fluides géothermiques) est aussi important pour la géologie, la géophysique et la géologie du pétrole. L'eau souterraine est un fluide visqueux (avec un nombre de Reynolds plus petit que 1) qui coule lentement (à l'exception près d'environnements géologiques particuliers comme les conduits karstiques parcourus par les rivières souterraines, les alluvions très grossières et les roches fracturées). Beaucoup de lois déduites empiriquement de l'eau souterraine peuvent également être déduites de la mécanique des fluides par le cas particulier de flux de Stokes où l'on considère des termes de viscosité et de pression, mais pas d'inertie.
Les relations mathématiques utilisées pour décrire le flux de l'eau à travers un milieu poreux sont l'équation de diffusion et l'équation de Laplace. Ces deux équations ont des applications dans plusieurs champs différents. Le flux régulier de l'eau, décrit par l'équation de Laplace, a été simulé grâce à des analogies d'électricité, d'élasticité et de conduction thermique. Le flux de transition de l'eau souterraine est similaire à la diffusion de la chaleur dans un solide, de sorte que certaines solutions à des problèmes hydrologiques ont été adaptées de celles de la conduction thermique.
Traditionnellement, le mouvement de l'eau souterraine a été étudié indépendamment en hydrologie, en climatologie, en chimie et en microbiologie. Avec la maturation de l'hydrogéologie, les fortes interactions entre l'eau souterraine, l'eau de surface, la géochimie, l'humidité du sol et le climat deviennent de plus en plus claires.
Définitions et propriétés
Article principal: aquifère
Un aquifère est au sens strict une formation géologique perméable qui contient et transporte de l'eau, par opposition à un aquitard ou un aquiclude qui sont tous deux peu perméables (mais la distinction entre les deux termes prête à confusion). On parle généralement d'aquitard pour désigner une formation géologique peu perméable (relativement à la formation considérée comme perméable). On gardera ici à l'esprit que le caractère perméable d'une formation géologique est relatif. Un grès peut être considéré comme perméable par rapport à un niveau argileux, mais devient peu perméable si on le compare à des dépôts graveleux grossiers par exemple.
L'écoulement de l'eau souterraine peut être confiné (captif) ou non (libre). Dans ce cas, le niveau de la surface libre de l'écoulement souterrain peut se déplacer verticalement sans limite vers le haut (jusqu'à la surface topographique). Dans le premier cas, la présence d'un niveau peu perméable ne permet pas l'élévation du niveau de la surface libre. Dans le cas d'un écoulement libre, le potentiel hydraulique à la surface libre de l'écoulement est égal à l'altitude de ce point. Dans le cas d'un écoulement confiné, le potentiel hydraulique est supérieur ou égal à l'altitude du mur de la formation peu perméable située au-dessus de l'écoulement.
Dans le cas d'un écoulement confiné, l'aquifère est entièrement saturé en eau (saturation égale à 1 ou 100 %). On parle d'écoulement saturé. Dans le cas d'un écoulement libre, on distingue une partie de l'aquifère saturée en eau (c'est la zone saturée), et une partie pour laquelle la saturation est inférieure à 1, c'est la zone non-saturée qui est située au-dessus de la zone saturée. La zone de transition entre la zone saturée et la zone non-saturée est appelée la frange capillaire.
Potentiel hydraulique
Le gradient de potentiel hydraulique noté Φ est à l'origine du déplacement des masses d'eau - l'eau se déplaçant du potentiel le plus haut vers le plus bas. La loi de Darcy, valable uniquement pour les milieux saturés, postule que le débit d'eau à travers une surface donnée d'un aquifère est proportionnel au gradient hydraulique. Le rapport entre le débit unitaire q (ou vitesse de Darcy) et le gradient hydraulique i est la conductivité hydraulique K (perméabilité étant un terme à éviter) :
- avec .
Le potentiel est donné par l'équation de Bernoulli :
avec z l'élévation du point mesuré (énergie potentielle), p la pression du fluide de masse volumique ρ, v la vitesse du fluide ; g est l'accélération de la pesanteur valant 9,81 m/s2.
Le potentiel hydraulique est une propriété directement mesurable. Il peut être mesuré à l'aide d'un transducteur de pression. Cette valeur peut être négative dans le cas de la succion, mais elle est positive dans les aquifères saturés. Un enregistrement du potentiel hydraulique sur un puits et pendant un certain temps est appelé un hydrographe.
Porosité
article principal: Porosité.
La porosité (n) est une propriété directement mesurable d'un aquifère. C'est une fraction entre 0 et 1 qui indique la quantité d'espace vide entre des particules de sol libres ou dans une roche fracturée. On peut la mesurer par extraction de l'eau (Veau) d'un volume d'aquifère saturé (Vtotal) :
- , entre 0 et 1.
Il faut distinguer l'existence de ces vides, de leur interconnexion (qui, elle, permet à un fluide de circuler). On parle de porosité efficace pour désigner les vides connectés entre eux.
On distingue :
- la porosité de matrice, liée à l'agencement des vides entre les grains dans les roches sédimentaires (30 % pour les sables et grès, 1 % pour les roches cristallines) ;
- la porosité de fractures, liée aux diaclases et fractures, typiquement dans les roches endogènes de type granite. Les fractures y sont souvent conjuguées, ce qui permet un réseau connecté, sauf si bouché par de l'argile ;
- la porosité de type karstique liée à la formation de grands vides dans les roches calcaires ou gypseuses (craie, calcaires, sel).
La porosité n'affecte pas directement la distribution des potentiels hydrauliques dans un aquifère, mais elle a un effet très fort sur la migration de contaminants, parce qu'elle affecte la vitesse du flux de l'eau souterraine par une relation proportionnelle inverse.
Contenu en eau
Le contenu en eau θ (ou teneur en eau) est une propriété directement mesurable. Elle représente la fraction de la roche qui est pleine d'eau liquide. C'est une fraction entre 0 et 1, et elle doit être inférieure ou égale à la porosité totale.
Le contenu en eau est très important en hydrologie de la zone vadose où la conductivité hydraulique est une fonction fortement non-linéaire du contenu en eau. Cela complique la solution de l'équation de l'écoulement non-saturé de l'eau souterraine.
Conductivité hydraulique
La conductivité hydraulique K et la transmissivité (T) sont des propriétés indirectes de l'aquifère. T est égale à K intégré sur l'épaisseur verticale (b) de l'aquifère :
- .
Ces propriétés sont des mesures de la capacité d'un aquifère à conduire l'eau. La perméabilité intrinsèque κ est une propriété secondaire du milieu. Elle ne dépend pas de la viscosité ni de la densité du fluide :
avec µ la viscosité cinématique du fluide (eau douce, eau salée ou pétrole), ρ la masse volumique du fluide et g l'accélération de la pesanteur.
Coefficient d'emmagasinement et porosité de drainage
Le coefficient d'emmagasinement spécifique Ss et son équivalent intégré sur l'épaisseur de l'aquifère, le coefficient d'emmagasinement S, permettent de déterminer les réserves d'une nappe captive. S indique le volume d'eau évacué par la nappe par unité de surface et par unité de charge ; il varie entre 0 et 1.
La production d'eau dans une nappe captive se fait sous l'influence de deux phénomènes : la décompression de l'eau et le tassement du milieu poreux qui la contient.
La porosité de drainage ωd (qui varie également entre 0 et 1) (ωd ≤ porosité effective) indique le volume d'eau évacué par le drainage d'une nappe libre dû à un abaissement d'une unité de son niveau piézométrique par unité de surface. Généralement ωd est de plusieurs ordres de grandeur plus grand que S. la porosité effective est souvent utilisée comme borne supérieure de la porosité de drainage.
Équations fondamentales d'état
Loi de Darcy
La loi de Darcy est une équation (obtenue empiriquement par Henry Darcy en 1856) qui énonce que la quantité d'eau du sol déchargée à travers une portion donnée de l'aquifère est proportionnelle à l'aire qui sectionne le flux, le gradient de portion hydraulique et la conductivité hydraulique.
Équation de flux d'eau du sol
L'équation de flux d'eau du sol, dans sa forme la plus générale, décrit le mouvement de l'eau du sol dans un milieu poreux (un aquifère ou un aquitard). Elle est connue en mathématique sous le nom d'équation de diffusion, et elle a beaucoup d'analogue dans d'autres branches. Beaucoup de solutions du flux d'eau du sol ont été empruntées ou adaptées de solutions existantes de la conduction thermique.
Elle est souvent dérivée d'un base physique en utilisant la loi de Darcy et la conservation de la masse pour un petit volume de contrôle. L'équation est souvent utilisée pour prédire un flux vers des puits, qui ont une symétrie radiale, de sorte que l'équation de flux est communément résolue avec des coordonnées polaires ou cylindriques.
Le test d'aquifère est l'une des solutions les plus utilisées et les plus fondamentales de l'équation de flux d'eau du sol. Elle peut être utilisée pour prédire l'évolution de la tête due à l'effet d'un pompage ou de plusieurs puits de pompage.
La solution de Thiem résout l'équation de flux de l'eau de sol à l'équilibre (équation de Laplace). L'équilibre réel est rarement atteint en réalité à moins de la présence de larges sources d'eau proches (un lac ou une rivière).
Cartographie hydrogéologique
Elle permet de rendre visible la localisation des aquifères du territoire, ce qui est notamment nécessaire pour la protection des champs captants et des périmètres de captages exploitées ou susceptibles de l'être pour l'alimentation en eau potable, l'irrigation et l'industrie. Elle est destinée aux élus, techniciens, et aux enseignants, chercheurs, universitaires, etc.
En France cette carte a été publiée en 1978. Elle devrait être entièrement mise à jour en , sur la base de la nouvelle version du référentiel hydrogéologique français (par le BRGM)[1]. Un échantillon en a été présenté en 2014. La nouvelle échelle et résolution seront plus précises, l'échelle passant de 1/1 500 000 (1 cm pour 15 km) à 1/1 000 000 (1 cm pour 10 km)[1].
Ce travail s'appuie sur la Base de données "BD Lisa" qui contient les limites des systèmes aquifères et qui découpe le territoire en unités hydrogéologiques (selon le type de formation géologique et leur perméabilité)[1]. La carte présente aussi une « zonation climatique fournie par Météo France qui donne une indication sur la recharge des aquifères par les précipitations, mais aussi des données ponctuelles localisant, entre autres, les forages géothermiques et les sources thermales »[2].
Notes et références
- « Nouvelle carte hydrogéologique de la France », sur BRGM (consulté le )
- « Nouvelle carte hydrogéologique de la France : présentation en avant-première », sur BRGM (consulté le )
Voir aussi
Bibliographie
- Banton, O. & Bangoy, L.-M. (1997) - Hydrogéologie, Multiscience environnementale des eaux souterraines, Presses de l'Université du Québec/AUPELF
- Castany, G. (1982) - Hydrogéologie Principes et méthodes, Dunod, Paris
- Castany, G. (1991) - « Origine et évolution des concepts des eaux souterraines », Travaux du comité français d'histoire de la géologie 3e série t. V no 1 (ISSN 1156-2919), Comité français d'histoire de la géologie, Paris, p. 1-7
- Detay, M. (1993) - Le forage d'eau, Masson, Paris
- Éric Gilli, Christian Mangan et Jacques Mudry, Hydrogéologie, Objets, méthodes, applications, Paris, Dunod, (lire en ligne)
- Imbeaux, É. :
- (1910) - « Les nappes aquifères de France - Essai d'hydrogéologie », sur Biodiversity Heritage Library (consulté le ), Bulletin de la Société géologique de France, 4e série, tome X], Société géologique de France, Paris, p. 180-244
- (1930) - « Essai d'hydrogéologie. Recherche, étude et captage des eaux souterraines », sur Gallica (consulté le ), Paris, Dunod, 704 p.
- Marsily, G. (1981) - Hydrogéologie quantitative, Masson
- Margat, J., Pennequin, D. & Roux, J.-C. (2013) - Histoire de l'hydrogéologie française, Association internationale des hydrogéologues - Comité français d'hydrogéologie (AIH-CFH), Orléans, 221 p.
Articles connexes
- Édouard Imbeaux (1861-1943), l'un des pères de l'hydrogéologie
- Généralités
- Concepts
- Modélisation
Liens externes
- Comité Français d'Hydrogéologie (CFH-AIH), http://www.cfh-aih.fr/
- Laboratoire d'hydrogéologie, Université d'Avignon
- Liens vers colloques hydrogéologie d'EDF pour 2006, 2007, 2008, 2009, 2010, 2011
- Portail de la géologie
- Portail de l’eau