Fonction linéaire (analyse)
Dans les mathématiques élémentaires, les fonctions linéaires sont parmi les fonctions les plus simples que l'on rencontre. Ce sont des cas particuliers d'applications linéaires.
Elles traduisent la proportionnalité.
Par exemple, on dira que le prix d'un plein d'essence est fonction linéaire du nombre de litres mis dans le réservoir car :
- pour zéro litre, on paie zéro euro ;
- pour un litre, on paie 1,40 euro ;
- pour 2 litres on paie 2,80 euros ;
- pour 10 litres on paie 14 euros ;
- pour 100 litres on paie 140 euros ;
- et pour N litres, on paie 1,4 × N euros.
Remarque : Faux-ami avec le français, les termes allemands Lineare Funktion et anglais Linear function désignent une fonction affine.
Comment reconnaître une fonction linéaire ?
Une fonction linéaire est définie de la manière suivante :
- avec y = ax
où le nombre a est un réel quelconque. Ce réel a s'appelle le coefficient de proportionnalité.
En repartant de l'égalité y = ax, on voit que pour x différent de zéro, on peut diviser les deux membres par x. Il vient donc :
Il suffit donc d'une valeur x non nulle et de son image y pour déterminer la valeur du coefficient de proportionnalité.
Représentation dans le plan
La représentation graphique d'une fonction est l'ensemble des points de coordonnées (x, y) tels que y = f(x).
Les fonctions linéaires définies de ℝ dans ℝ se représentent dans le plan par une droite. Cette droite passe par l'origine du repère. En effet, si M est un point de la représentation graphique tel que x = 0, il vient nécessairement y = 0.
L'élément graphique important est le coefficient directeur (ou pente) de la droite. Il correspond au coefficient de proportionnalité de la fonction linéaire. On retrouve alors un moyen simple de calcul de ce coefficient directeur : si M(x, y) est un point de la droite différent de l'origine, nous avons, comme précédemment y = ax puis, par division par x (non nul)
Il existe un moyen de lire sur le graphique la pente de la droite : c'est l'inclinaison de la droite par rapport à l'axe des abscisses.

Par exemple :
- si a = 1, la droite fait, dans un repère orthonormé, un angle de 45° avec l'axe des abscisses (il s'agit de la première bissectrice du repère, représentation graphique de la fonction identité) ;
- si a = 2, la droite « monte » plus fortement que pour a = 1 ;
- si a = 0, la droite est confondue avec l'axe des abscisses (représentation graphique de la fonction nulle) ;
- si a = –1, la droite « descend ».
En résumé :
- si a > 0, la droite « monte » quand on la lit de gauche à droite ;
- si a = 0, la droite est confondue avec l'axe des abscisses ;
- si a < 0, la droite « descend » quand on la lit de gauche à droite.
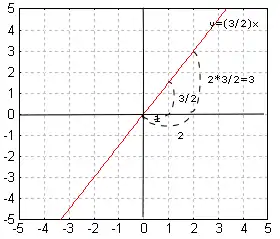
Dans un quadrillage à l'unité, le coefficient directeur correspond au nombre de carreaux parcourus sur l'axe des ordonnées lorsqu'on se déplace d'un seul carreau (vers la droite) sur celui des abscisses.
Opérations
Somme
Considérons deux fonctions linéaires f et g définies, pour tout réel x, par :
Alors, pour tout réel x, on a
Autrement dit, la somme de deux fonctions linéaires est une fonction linéaire.
Multiplication par un réel
Considérons la fonction linéaire f définie pour tout réel x par f(x) = ax et k un réel quelconque. Alors, pour tout réel x, on a
Par conséquent, le produit d'une fonction linéaire par une constante est une fonction linéaire.
Produit
Considérons deux fonctions linéaires f et g définies, pour tout réel x, par :
On a alors :
Autrement dit, le produit de deux fonctions linéaires non nulles n'est pas une fonction linéaire mais une fonction du second degré.
Dérivée
Soit f une fonction linéaire. La tangente à la droite représentative de la fonction f est en tout point de cette droite elle-même, si bien que pour tout réel x, on a :
La fonction dérivée de f est donc la fonction constante définie sur ℝ par cette équation.
Intégrale
Soit f une fonction linéaire, positive sur l'intervalle [a, b]. On peut calculer l'intégrale de f sur [a, b] en utilisant la formule de l'aire d'un trapèze (somme des bases multipliée par la hauteur et divisée par 2) :
soit, pour :
Primitives
Soit f une fonction linéaire définie par f(x) = ax. Alors il existe une infinité de primitives de cette fonction ; elles sont toutes définies par des expressions de la forme :
où C est une constante réelle quelconque.
Parité
Soit f une fonction linéaire définie par f(x) = ax. Pour tout réel x, on a :
Donc une fonction linéaire est toujours impaire. Il existe une seule fonction linéaire qui soit de plus paire : c'est la fonction nulle, qui est constante.
Propriétés caractéristiques
Une fonction linéaire vérifie toujours la propriété: Pour tout réel et tout réel , Cette propriété est caractéristique de la fonction linéaire, c'est-a-dire qu'une fonction numérique vérifiant cette propriété est une fonction linéaire, son coefficient de proportionnalité a est f(1).
Une fonction linéaire vérifie toujours la propriété: Pour tout réel et tout réel , Cette propriété, étudiée dans l'équation fonctionnelle de Cauchy, est caractéristique de la fonction linéaire pour peu qu'on la complète avec une condition de régularité (fonction continue en un point ou fonction majorée sur un intervalle de longueur non nulle ou fonction monotone sur un intervalle de longueur non nulle...).
Voir aussi
- Portail de l'analyse