Faisceau de cercles

Étant donné un cercle (c₀) et une droite (d), il existe une infinité de cercles (c) tels que l'axe radical de chacun d'eux et du cercle (c₀) soit la droite (d). On dit que ces cercles (et le cercle c₀) forment un faisceau.

Un faisceau est déterminé par deux cercles (c₁) et (c₂) non concentriques.

Les centres des cercles (c) sont situés sur la droite (Δ) perpendiculaire à (d) passant par le centre de (c₀). (Δ) est la droite des centres du faisceau.

Deux cercles quelconques (c₁) et (c₂) du faisceau admettent (d) comme axe radical.

Un faisceau est déterminé par deux cercles (c₁) et (c₂) non concentriques.

Faisceau à points de base

Si les deux cercles sont concourants, alors le faisceau de cercles est l'ensemble des cercles passant par ces deux points A et B. La droite (AB) est l'axe radical.

La droite des centres des cercles du faisceau est alors la médiatrice du segment [AB].

Faisceau de cercles tangents

Si les deux cercles sont tangents en un point I, alors le faisceau de cercles est l'ensemble des cercles tangents à la droite perpendiculaire en I à la droite O₁O₂ et passant par I. Cette droite est l'axe radical.

Faisceau à points limites (points de Poncelet)

Si les deux cercles ne sont pas concourants, on parle de faisceau de Poncelet.

Les deux points limites (cercles de rayon nul du faisceau) U et V sont les projections orthogonales des points d'intersection des tangentes aux cercles (c₁) et (c₂) sur la droite O₁O₂. Ces deux points sont appelés points limites ou points de Poncelet.

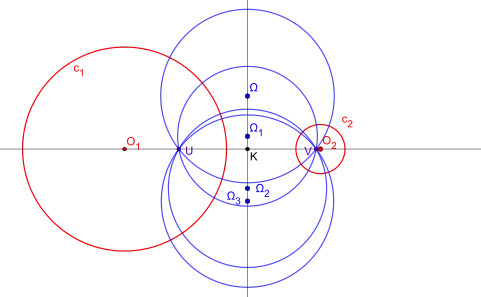
Étant donné deux cercles (c) et (c₁) non concentriques, il existe une infinité de cercles (γ) orthogonaux à (c) et (c₁), ils sont aussi orthogonaux à tous les cercles du faisceau déterminé par (c) et (c₁).

Les cercles (γ) orthogonaux aux cercles (c) d'un faisceau F forment un faisceau Φ conjugué de F. L'axe radical d'un des faisceaux est la droite des centres de l'autre.

Si l'un des faisceaux est formé de cercles tangents, il en est de même de l'autre. Sinon si l'un des faisceaux est à points de base, l'autre est à points limites, et il y a identité entre ces couples de points.

Dans un repère orthonormé, l'équation cartésienne d'un cercle peut se mettre sous la forme ${\displaystyle x^{2}+y^{2}+ax+by+c=0}$ ; si le second cercle a pour équation ${\displaystyle x^{2}+y^{2}+a'x+b'y+c'=0}$, on voit que l'axe radical aura pour équation ${\displaystyle (a-a')x+(b-b')y+c-c'=0\iff Ax+By+C=0}$, et que tous les cercles d'équation ${\displaystyle x^{2}+y^{2}+(a+At)x+(b+Bt)y+c+Ct=0}$ auront le même axe radical ; cette famille d'équations définit un faisceau de cercles (pour les valeurs de ${\displaystyle t}$ pour lesquelles l'équation possède des solutions réelles).

Plus généralement, étant donné deux courbes algébriques d'équations ${\displaystyle A:P(x,y)=0}$ et ${\displaystyle B:Q(x,y)=0}$, le faisceau (linéaire) de base ${\displaystyle (A,B)}$ est l'ensemble des courbes d'équation ${\displaystyle aP(x,y)+bQ(x,y)=0}$ (${\displaystyle P}$ et ${\displaystyle Q}$ étant des polynômes) ; on se place souvent dans le cadre projectif, prenant alors des polynômes homogènes de la forme ${\displaystyle P(X,Y,T)}$.