Effet Hall

L'effet Hall « classique » a été découvert en 1879 par Edwin Herbert Hall[1], qui l'a énoncé comme suit : « un courant électrique traversant un matériau baignant dans un champ magnétique, engendre une tension perpendiculaire à ce dernier ».

Illustration de l'effet Hall pour différents sens du courant et du champ magnétique.
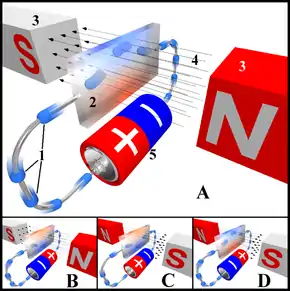
Légende :
1. Électrons
2. Élément ou capteur à effet Hall
3. Aimants
4. Champ magnétique
5. Source de courant
Dans le dessin A, une charge négative apparait à la bordure haute de l'élément (couleur bleue), et une charge positive à sa bordure basse (couleur rouge). En B et C, l'inversion du sens du courant ou de celui du champ magnétique provoque l'inversion de cette polarisation. En D, la double inversion du courant électrique et du champ magnétique donnent à l'élément la même polarisation qu'en A.

Sous certaines conditions, cette tension croît par paliers, effet caractéristique de la physique quantique, c'est l'effet Hall quantique entier ou l'effet Hall quantique fractionnaire.

Dynamique électronique dans le vide

Avant de voir comment les électrons se comportent dans un solide, rappelons ce qu'il se passe lorsqu'un électron, de charge $-e$ et de masse $m_{e}$ placé dans le vide, est soumis à un champ électrique ${\overrightarrow {E}}$ et/ou à un champ magnétique ${\overrightarrow {B}}$ .

Dans de telles conditions, l'électron subit une force appelée force de Lorentz :

{\overrightarrow {F_{lorentz}}}=-e{\overrightarrow {E}}-e{\overrightarrow {v_{e}}}\wedge {\overrightarrow {B}}

où ${\overrightarrow {v_{e}}}$ est la vitesse de l’électron.

Électron soumis à un champ électrique ${\overrightarrow {E}}$ , et sous champ magnétique nul ${\overrightarrow {B}}={\overrightarrow {0}}$

Soit un champ électrique ${\overrightarrow {E}}$ uniforme. D’après le principe fondamental de la dynamique (dans un référentiel galiléen), on a :

m_{e}{\frac {d{\overrightarrow {v_{e}}}}{dt}}={\overrightarrow {F_{lorentz}}}=-e{\overrightarrow {E}}

D'où :

{\overrightarrow {v_{e}}}={\frac {-et}{m_{e}}}{\overrightarrow {E}}+{\overrightarrow {v_{0}}}

avec ${\overrightarrow {v_{0}}}$ vitesse initiale de l'électron.

Sous l’action unique du champ électrique constant, l’électron est uniformément accéléré dans la direction du champ électrique.

Électron soumis à un champ magnétique ${\overrightarrow {B}}$ , et sous champ électrique nul ${\overrightarrow {E}}={\overrightarrow {0}}$

Soit un champ magnétique dirigé selon $z$ , ${\overrightarrow {B}}={\begin{vmatrix}0\\0\\B\end{vmatrix}}$

Le champ magnétique ne fournit pas d'énergie à l'électron car la force magnétique est perpendiculaire au mouvement, son travail est donc nul $(W={\overrightarrow {B}}.{\overrightarrow {v}}=0)$ .

D'après le théorème de l'énergie cinétique, sa vitesse reste donc constante :

d{E_{c}}=-e.({\overrightarrow {v}}\wedge {\overrightarrow {B}}).{\overrightarrow {v}}dt=0

L'accélération de l'électron est perpendiculaire à la trajectoire car la force est perpendiculaire à la vitesse (donc à la trajectoire).

De plus, si l'électron possède une vitesse constante, les composantes de l'accélération dans le repère de Frenet sont rapides à déterminer.

Il est possible de démontrer que le mouvement forme un cercle de rayon $R=v{\frac {m}{eB}}$ , autour de l’axe du champ magnétique ( $z$ dans notre exemple).

Dans cette description classique, l’électron peut avoir une orbite de taille quelconque car il peut avoir n’importe quelle vitesse.

La période de rotation pour effectuer un tour complet est donnée par :

T={\frac {2\pi R}{v}}=2\pi {\frac {m_{e}}{eB}}={\frac {2\pi }{w_{c}}}

avec $w_{c}={\frac {eB}{m_{e}}}$ la pulsation cyclotron de l’électron.

En conclusion, sous l’influence d’un champ électrique, un électron est accéléré dans la direction du champ et, sous l’influence d’un champ magnétique, il est mis en rotation uniforme autour de l’axe du champ magnétique.

Dynamique électronique dans un matériau

La dynamique électronique au sein d'un matériau conducteur découle du modèle de Drude.

Principe

Principe de l'effet Hall dans un conducteur filiforme à section rectangulaire.

Force magnétique de Lorentz et force électrique de Hall dans un conducteur parcouru par un courant et soumis à un champ magnétique.

L'effet Hall

Schéma présentant l'évolution des porteurs dans un métal lorsqu'il est soumis à la fois à un champ électrique et à un champ magnétique

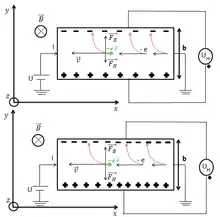
L’effet Hall trouve son origine dans la nature du courant qui traverse un matériau conducteur. Ce courant est le résultat du mouvement d’un grand nombre de porteurs de charges (combinaison d'électrons, trous et ions).

En présence d’un champ électrique, dirigé selon la direction $x$ , les porteurs de charges acquièrent une vitesse de dérive moyenne stationnaire qui est limitée par les collisions avec les impuretés du matériau et/ou les phonons. Dans ces conditions, les porteurs de charges ont une trajectoire en moyenne rectiligne. C’est ce principe qui génère un courant électrique.

Lorsqu’on ajoute un champ magnétique de composante perpendiculaire au déplacement des électrons, dans cet exemple, selon l’axe $z$ , les porteurs de charges sont, en plus d’être accélérés, mis en rotation autour de l’axe du champ magnétique.

Dans certaines conditions, les porteurs de charges n’ont pas le temps de décrire un cercle complet autour de l’axe du champ magnétique. De ce fait, dès l’application du champ magnétique, les porteurs de charges ne pouvant pas sortir du solide vont s’accumuler sur une des faces du matériau.

Cette accumulation de charges se traduit par l’apparition d’un champ électrique, selon la direction $y$ , nommé champ de Hall.

Ce champ électrique engendre sur les porteurs de charges une nouvelle force qui tend à diminuer la force de Lorentz (responsable de la mise en rotation des porteurs de charges).

Au bout d’un temps assez court, le champ de Hall est suffisamment grand pour compenser la déviation des électrons. Le régime stationnaire est atteint, les porteurs de charges ne sont plus déviés par le champ magnétique. Une tension fixe est apparue sur les faces du solide, nommée tension de Hall.

Par sa définition et son origine, l’effet Hall dépend du courant ( $I$ ) induit dans le matériau par le champ électrique, du champ magnétique ( ${\vec {B}}$ ) appliqué au matériau, mais également de la géométrie du matériau. En effet, plus ce dernier est « étroit » plus les porteurs de charges auront du mal à faire une rotation complète autour de l’axe du champ magnétique.

La tension de Hall dans un échantillon conducteur de forme parallélépipédique est égale à :

U_{H}=R_{H}{\frac {IB}{a}}

où $a$ est l'épaisseur de matériau dans la direction du champ magnétique (ici $z$ )

L'effet Hall dans un métal

Dans un métal, les porteurs sont majoritairement des électrons. De ce fait, la constante de Hall a pour valeur

R_{H}=-{\frac {1}{ne}}

, où n représente le nombre d’électrons par unité de volume qui est égale à 10²³ e/cm³

Il est judicieux de remarquer que la tension de Hall est proportionnelle au coefficient de Hall $R_{H}$ , lui-même inversement proportionnel à $n$ dans le matériau.

Plus un matériau possède de porteurs de charge et plus la tension de Hall qui peut potentiellement apparaitre est faible. C'est pourquoi on utilise des semi-conducteurs dans les applications de l'effet Hall.

L'effet Hall dans un semi-conducteur

Étant donné que l’effet Hall dépend du nombre de porteurs de charges, on peut noter que cet effet est plus important dans un semi-conducteur que dans un métal. En effet, les semi-conducteurs possèdent en plus des porteurs de charges négatifs (électrons), des porteurs de charges positifs (trous).

On peut donc exprimer de la même manière que dans un métal, la tension de Hall dans un semi-conducteur, et de ce fait en déduire certaines caractéristiques intrinsèques au matériau semi-conducteur.

Les équations ci-dessous récapitulent quelques paramètres importants quantifiables grâce à l’effet Hall (mesure de la tension de Hall).

Électrons: ${\overrightarrow {v}}=-\mu _{n}{\overrightarrow {E}}$ avec $\mu _{n}$ la mobilité des électrons dans le matériau; $R_{H}=-{\frac {1}{ne}}$; $\sigma =ne\mu _{n}=-{\frac {\mu _{n}}{R_{H}}}$ avec $\sigma$ la conductivité du matériau

Trous: ${\overrightarrow {v}}=+\mu _{p}{\overrightarrow {E}}$ avec $\mu _{p}$ la mobilité des trous dans le matériau; $R_{H}=+{\frac {1}{pe}}$; $\sigma =pe\mu _{p}=+{\frac {\mu _{p}}{R_{H}}}$ avec $\sigma$ la conductivité du matériau

Applications

Les capteurs à effet Hall permettent de mesurer :

les champs magnétiques (teslamètres à sondes) ;
l'intensité des courants électriques : capteur de courant à effet Hall (exemple : pince ampèremétrique à effet Hall).

Ils permettent également la réalisation de capteurs ou des détecteurs de position sans contact, utilisés notamment dans l'automobile, pour la détection de position d'un arbre tournant (boîte de vitesses, cardans, etc.).

Des capteurs à effet Hall existent dans les systèmes de mesure de vitesse pour, entre autres, le matériel ferroviaire ou permettant de connaître précisément la position du rotor des moteurs de type brushless.

On trouve également des capteurs à effet Hall sous les touches des claviers d'ordinateur ainsi que sous les touches des instruments de musique modernes (orgues, orgues numériques, synthétiseurs) évitant ainsi l'usure que subissaient les contacteurs électriques traditionnels.

L'effet Hall est parfois utilisé dans le domaine des satellites artificiels, plus précisément dans la conception des propulseurs de ces satellites (propulseur à effet Hall[2]).

Notes et références

(en) Edwin Herbert Hall, « On a New Action of the Magnet on Electric Currents », American Journal of Mathematics, vol. 2, n^o 3,‎ 1879, p. 287-92 (DOI 10.2307/2369245, JSTOR 2369245, lire en ligne, consulté le 13 octobre 2010).
Vidéo vulgarisatrice sur l'effet hall dans les moteurs ioniques.

Voir aussi

Bibliographie

(en) T. Ando, Y. Arakawa, K. Furuya, S. Komiyama, H. Nakashima , Mesoscopic physics and electronics, Springer, 1998 (ISBN 978-3-642-71978-3).
Edward M. Purcell, Claude Guthmann, Pierre Lallemand, Berkeley : cours de physique 2 – Électricité et magnétisme, Paris, Dunod, 1998 (ISBN 978-2-10-004060-5).

Articles connexes

Liens externes

Simulation paramétrable de l'effet Hall.
Séminaire Bourbaphy.
L'effet Hall, sciences.univ-nantes.fr.

Portail de la physique
Portail de l’électricité et de l’électronique

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[1] (en) Edwin Herbert Hall, « On a New Action of the Magnet on Electric Currents », American Journal of Mathematics, vol. 2, n^o 3,‎ 1879, p. 287-92 (DOI 10.2307/2369245, JSTOR 2369245, lire en ligne, consulté le 13 octobre 2010).

[Video_vulgarisatrice_sur_l'effet_hall_dans_les_moteurs_ioniques-2] Vidéo vulgarisatrice sur l'effet hall dans les moteurs ioniques.