Croissance exponentielle
En mathématiques, en économie et en biologie, on parle d'un phénomène à croissance exponentielle (ou géométrique) lorsque la croissance en valeur absolue de la population est proportionnelle à la population existante, c'est-à-dire lorsque le taux de croissance intrinsèque est constant et positif.
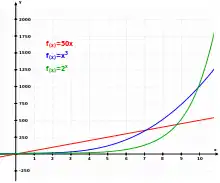
Principe
On exprime alors souvent la croissance sous forme d'un pourcentage : une croissance de 10 % par an signifie que la population est multipliée par 1,1 chaque année. Ainsi, pour une population initiale de 1 000 individus :
- au bout d'un an, elle passe à 1 100 individus () ;
- au bout de deux ans, elle passe à 1 210 individus ( ou ou ) ;
- …
- au bout de 7 ans, elle a quasiment doublé (la partie entière de est ) ;
- …
- au bout de 100 ans, elle a été multipliée par 13 780 ;
- la formule générale est pour estimer la population après n années ayant une population de départ Pop0, et où croissance est le facteur multiplicatif permettant de passer d'une population à la population l'année suivante.
Croissance exponentielle continue et taux de croissance intrinsèque
Lorsque le phénomène de croissance exponentielle est continu, on peut le modéliser au moyen d'une fonction exponentielle
où N(t) est le nombre d'individus au temps t, N(0) le nombre d'individus au temps 0, r le taux de croissance intrinsèque et t le temps, e étant la constante d'Euler valant approximativement 2,718.
La notion de taux de croissance se décline de deux façons : le taux de croissance effectif et le taux de croissance intrinsèque. Une population avec un taux de croissance effectif de 10 % par siècle a un taux de croissance intrinsèque pour cette même période d'environ 9,53 %, car 1,1 ≈ e0,0953 tandis qu'un taux de croissance intrinsèque annuel de 100 % signifie que la population sera multipliée par environ 2,72 en un an, soit un taux de croissance annuel de 172 % alors qu'un taux de croissance annuel de 100 % signifie que la population a doublé en un an et donc que le taux de croissance intrinsèque annuel est de ln(2) soit environ 69 %.
Contrairement aux taux de croissance effectifs qui se multiplient, les taux de croissance intrinsèque s'ajoutent. Ainsi un taux de croissance intrinsèque constant mensuel de 5 % correspond à taux de croissance intrinsèque annuel de 60 %. Ceci provient du fait que ces taux apparaissent en exposant.
Pour une même période de référence, le taux de croissance effectif μ et le taux de croissance intrinsèque r sont liés par la relation : 1 + μ = er.
Explosion exponentielle et ses limites
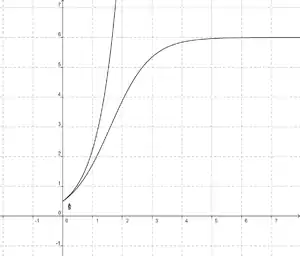
Avec une croissance exponentielle la taille de la population augmente de plus en plus vite ; on parle de ce fait parfois d'explosion exponentielle. Cela donna lieu au mythe du brahmane Sissa (3 000 ans avant notre ère).
Cette évolution théorique ne résiste donc pas à l'expérience : aucun phénomène ne peut croître indéfiniment car sa croissance est limitée par le milieu dans lequel se trouve la population. Le premier à avoir soulevé un tel problème fut le pasteur Thomas Malthus en 1798 dans son Essai sur le principe de population, bien que ses prévisions sur la croissance de la population humaine ne se soient pas réalisées.
De nos jours, on admet volontiers que le développement de micro-organismes d'une culture microbiologique peut être modélisé sous forme exponentielle pour le début du développement : le premier organisme se divise en deux organismes filles, qui se divisent ensuite chacun pour en former quatre, qui se séparent pour en former huit, et ainsi de suite. Mais les contraintes du milieu (nutriment épuisé ou volume disponible atteint) rendent préférable, par la suite, le choix d'un modèle de Verhulst (1838) qui s'exprime ainsi :
- dans le domaine du continu
- dans le cas discret
avec tout le caractère chaotique que peut présenter une telle suite logistique.
Exemples
Voici quelques cas emblématiques de croissance exponentielle :
- le nombre de malades du Covid-19 lors de la phase d'expansion de la pandémie de 2020, avant toute mesure pour aplanir la courbe[1],[2] ;
- l'augmentation du nombre de micro-organismes (exemple cité ci-dessus) et des organismes ;
- les nouvelles réactions lors des phénomènes de réaction en chaîne.
 Les bactéries présentent une croissance exponentielle dans des conditions optimales.
Les bactéries présentent une croissance exponentielle dans des conditions optimales.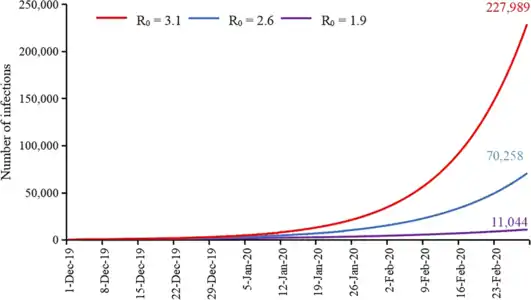 Estimation du nombre de cas de COVID-19 à Wuhan (phase d'expansion) en fonction du taux de reproduction de base
Estimation du nombre de cas de COVID-19 à Wuhan (phase d'expansion) en fonction du taux de reproduction de base
Références
- Étienne Ghys, « Epidémies : aplatir les exponentielles », Le Monde, (lire en ligne), voir aussi la version sur la page personnelle de l'auteur.
- Etienne Meyer-Vacherand, « Covid-19 : comprendre la croissance exponentielle d’une pandémie, un défi cognitif pour la population », Le Monde, (lire en ligne)
Voir aussi
Articles connexes
Lien externe
- « Fonction exponentielle : à tout Euler », La Méthode scientifique, France Culture, 19 novembre 2020.
- Portail des mathématiques
- Portail de l’économie