Courbe cubique

En mathématiques, une courbe cubique est une courbe plane définie par une équation du troisième degré

${\displaystyle F(X,Y,Z)=0}$

Quelques courbes cubiques. Voir les informations sur l'image pour les détails.

Cubique avec point singulier

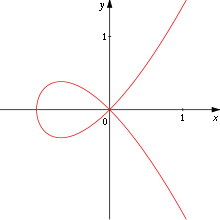
en les coordonnées homogènes [X:Y:Z] du plan projectif; ou bien c'est la version non homogène pour l'espace affine obtenue en faisant Z = 1 dans une telle équation. Ici F est une combinaison linéaire non nulle des monômes de degré trois

X³, X²Y, ..., Z³

en X,Y et Z. Ceux-ci sont au nombre de dix; donc les courbes cubiques forment un espace projectif de dimension 9, au-dessus de n'importe quel corps commutatif K donné. Chaque point P impose une seule condition linéaire sur F, si nous demandons à C de passer par P. Donc nous pouvons trouver une courbe cubique passant par n'importe quelle famille de neuf points donnée à l'avance.

Si on cherche les cubiques qui passent par 8 points donnés, on obtient pour les coefficients de l'équation d'une telle cubique un système linéaire homogène de 8 équations à 10 inconnues, dont le rang est 8 au maximum. Si ces points sont "en position générale" (la géométrie algébrique est faite entre autres pour comprendre ce que cela veut dire) le rang est exactement 8.

Si alors ${\displaystyle C_{1}=0\,}$ et ${\displaystyle C_{2}=0\,}$ sont les équations de deux d'entre elles, les autres sont de la forme ${\displaystyle \lambda _{1}C_{1}+\lambda _{2}C_{2}=0\,}$. Elles passent toutes par les points d'intersection de ces deux cubiques ; il y a 9 tels points d'après le théorème de Bézout.

Nous venons de montrer, d'une façon un peu légère il est vrai, que toutes les cubiques planes qui passent par 8 points "en position générale" passent par un neuvième point. Ce résultat sert notamment à prouver l'associativité de la loi de groupe définie sur les cubiques non singulières, voir l'article courbe elliptique : il est également lié à la résolution du paradoxe de Cramer.

Une courbe cubique peut avoir un point singulier ; dans ce cas elle a une paramétrisation par une droite projective. Sinon une courbe cubique non singulière est connue pour avoir neuf points d'inflexion au-dessus d'un corps algébriquement clos tel que les nombres complexes. Cela peut être démontré en prenant la version homogène de la matrice hessienne définie une cubique, et en intersectant son déterminant avec C; les intersections sont alors comptées par le théorème de Bézout. Ces points ne peuvent cependant être tous réels, de sorte qu'ils ne peuvent pas être vus dans le plan projectif réel en traçant la courbe. Les points réels des courbes cubiques furent étudiés par Newton; ils forment un ou deux ovales.

Une cubique non singulière définit une courbe elliptique, sur tout corps K pour lequel elle a un point à coordonnées dans K (point K-rationnel). Les courbes elliptiques sur le corps des nombres complexes sont maintenant souvent étudiées en utilisant les fonctions elliptiques de Weierstrass. Ces fonctions elliptiques (pour un réseau donné) forment un corps isomorphe au corps des fonctions rationnelles d'une cubique d'équation affine ${\displaystyle y^{2}=x(x-1)(x-\lambda )}$ . La possibilité pour une cubique sur K d'avoir une telle forme de Weierstrass dépend de l'existence d'un point K-rationnel, qui sert comme point à l'infini dans la forme de Weierstrass. Par exemple, il y a plusieurs courbes cubiques qui n'ont pas de tel point, quand K est le corps des nombres rationnels.