Branche parabolique

Dans l'étude des courbes planes, il existe parfois des points de la courbe qui s'éloignent infiniment de l'origine du repère. L'étude de ces courbes dans ces zones s'appelle l'étude des branches infinies. Quand la courbe semble regarder dans une direction mais tout en s'en éloignant, on dit que la courbe possède une branche parabolique dont l'axe est donné par la direction que regarde la courbe.

Branches paraboliques
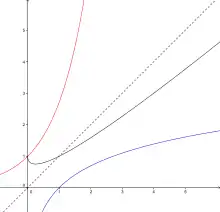
d'axe Ox - Courbe bleue :

y = ln(x)

,
d'axe Oy - Courbe rouge :

y = exp(x)

,
d'axe d :

y = x

- Courbe noire :

y = 1 + x - \sqrt x

.

Ce nom provient du fait que la portion de courbe ressemble alors à une portion de parabole.

Courbe représentative d'une fonction

On considère une fonction $f$ définie au voisinage de plus ou moins l'infini.

On dit que la courbe représentative de $f$ possède une branche parabolique d'axe (Oy) en plus l'infini (ou moins l'infini) si le quotient de $f (x)$ par $x$ tend vers l'infini en plus l'infini (ou moins l'infini) :

\lim _{x\to +\infty }{\frac {f(x)}{x}}=\pm \infty \quad \mathrm {ou} \quad \lim _{x\to -\infty }{\frac {f(x)}{x}}=\pm \infty

.

On dit que la courbe représentative de $f$ possède une branche parabolique d'axe d : $y = ax$ si le quotient de $f (x)$ par $x$ tend vers un réel $a$ mais que $f (x) - ax$ tend vers l'infini

\lim _{x\to +\infty }{\frac {f(x)}{x}}=a\quad \mathrm {ou} \quad \lim _{x\to -\infty }{\frac {f(x)}{x}}=a

et

\lim _{x\to +\infty }f(x)-ax=\pm \infty \quad \mathrm {ou} \quad \lim _{x\to -\infty }f(x)-ax=\pm \infty

Si la limite de $f (x) - ax$ est plus l'infini, la courbe regarde l'axe par au-dessus, si la limite est moins l'infini, la courbe regarde l'axe par en dessous.

Courbe paramétrée

On considère une courbe paramétrée d'équation

x=x(t)

y=y(t)

définie au voisinage de $t 0$ .

On recherche des branches paraboliques si

\lim _{t\to t_{0}}x(t)=\pm \infty \quad \mathrm {et} \quad \lim _{t\to t_{0}}y(t)=\pm \infty

.

La courbe possède une branche parabolique d'axe (Oy) si

\lim _{t\to t_{0}}{\frac {y(t)}{x(t)}}=\pm \infty

.

La courbe possède une branche parabolique d'axe d : $y = ax$ si

\lim _{t\to t_{0}}{\frac {y(t)}{x(t)}}=a

et

\lim _{t\to t_{0}}y(t)-ax(t)=\pm \infty

.

Équation polaire

Courbe d'équation polaire

\rho (\theta )={\frac {16}{(4\theta -\pi )^{2}}}

et sa branche parabolique d'axe d:y = x.

On considère une courbe définie par

\rho =\rho (\theta )

,

c'est-à-dire l'ensemble des points $M (x; y)$ tels que

x=\rho (\theta )cos(\theta )

y=\rho (\theta )\sin(\theta )

définie au voisinage de $θ 0$ .

On recherche des branches paraboliques si

\lim _{\theta \to \theta _{0}}\rho (\theta )=\pm \infty

.

La courbe possède une branche parabolique de direction faisant un angle $θ 0$ avec l'axe des $x$ si

\lim _{\theta \to \theta _{0}}\rho (\theta )\sin(\theta -\theta _{0})=\pm \infty

.

Voir aussi

Asymptote

Portail de l'analyse

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.