Les opérations bit à bit/Manipulations sur les puissances de deux

Dans cette section, nous allons aborder les opérations qui font intervenir des nombres de la forme $2^{n}$ et $2^{n}-1$ . Nous allons commencer par une opération assez simple, qui permet de calculer la puissance de $2^{n}$ qui est immédiatement supérieure à un nombre $x$ donné. Cette opération est à la base de calculs arithmétiques ou logiques plus complexes, comme le calcul du logarithme d'un nombre entier.

Modulo par une puissance de deux

Après avoir vu la multiplication et la division, nous pouvons maintenant passer au modulo par une constante. Nous allons nous concentrer sur le cas du modulo par une puissance de 2, les autres cas n'ayant pas de solution algorithmique simple. On peut d'or et déjà dire que ce modulo par une puissance de deux a un lien très fort avec la division par une puissance de deux. Cette dernière se traduisant par un décalage de n rangs, on peut se douter que le modulo aura un lien avec ces décalages. Nous allons d'abord voir le cas des nombres positifs, puis les nombres signés.

Nombres positifs

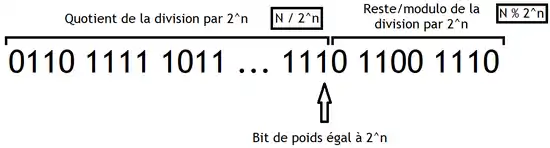
Le modulo par une puissance de deux se contente de garder les bits effacés par le décalage correspondant à la division. Pour comprendre comment faire ce calcul, nous allons reprendre, encore une fois, l'écriture en binaire d'un nombre :

2^{n}+2^{n-1}+2^{n-2}+...+2^{2}+2^{1}+2^{0}

Par définition, le modulo d'un nombre va prendre le reste de la division par un entier. Si calcule le reste modulo $2^{x}$ , cela veut dire qu'on doit supprimer tous les multiples de $2^{x}$ dans l'écriture binaire de notre nombre., en les mettant à zéro. En clair : pour obtenir le modulo, on doit mettre à zéro les n bits les plus à droite dans l'écriture binaire de notre nombre. Cette mise à zéro se fait en utilisant une opération ET, avec la constante égale à $2^{n}-1$ .

x\%2^{n}=x.(2^{n}-1)

Modulo et quotient d'une division par une puissance de deux en binaire.

Mais attention : pour ce qui est des nombres négatifs, le coup du AND ne marche pas. Mais on peut toujours prendre la valeur absolue de notre nombre, calculer le modulo avec un AND, et prendre l'opposé, cela marche tout aussi bien.

Nombres signés

Pour les nombres signés, la méthode précédente ne peut pas être utilisée directement. On est obligé de passer par l'intermédiaire de la valeur absolue et d'en calculer le modulo. Puis, il faut corriger le résultat en fonction de son signe. Dans ce qui va suivre, nous allons noter le bit de signe $y$ . Celui-ci sera mis dans un nombre, précisément dans son bit de poids faible.

Première méthode

Une première formule pour le calcul du modulo est la suivante :

$mod(n,2^{n})=\left\{{\begin{array}{r c l}x.(2^{n}-1)&x>=0\\-\left(-x.(2^{n}-1)\right)&x<0\\\end{array}}\right.$

Le calcul du modulo d'un nombre signé peut donc se réaliser avec l'équation suivante :

\left(abs(x).(2^{n}-1)\right)\oplus y-y

La seule exception est quand on souhaite calculer le modulo 2. Dans ce cas, le bit de poids faible donne directement le modulo, peu importe le signe du nombre testé. Le calcul est alors le suivant :

\left(x.1\right)\oplus y-y

Seconde méthode

Une autre solution est d'utiliser la formule suivante :

$mod(n,2^{n})=\left\{{\begin{array}{r c l}x.(2^{n}-1)&x>=0\\\left(x+y).(2^{n}-1)\right)-y&x<0\\\end{array}}\right.$

Le calcul du modulo d'un nombre signé peut donc se réaliser avec l'équation suivante :

\left(x+y).(2^{n}-1)\right)-y

Arrondir vers un multiple de $2^{n}$

Dans cette section, nous allons voir comment arrondir un nombre au multiple de $2^{n}$ immédiatement supérieur ou inférieur.

Arrondi au multiple inférieur

Pour le multiple immédiatement supérieur, prenons un exemple. Je souhaite arrondir 46 au multiple de 8 immédiatement supérieur : 46 sera arrondi à 48 (8 * 6). Si j'avais voulu arrondir au multiple immédiatement inférieur, j'aurais obtenu 40 (8 * 5). Le plus simple, c'est arrondir au multiple de $2^{n}$ immédiatement inférieur. Pour cela, il suffit de mettre les n bits les plus à droite à 0, en utilisant un masque. Exemple : je veux arrondir x au multiple de 8 inférieur. Dans ce cas, je dois faire : $x.1111111...111000$ . Si on regarde bien, cela revient à appliquer un AND entre le nombre à arrondir et une constante qui vaut : ${\overline {2^{n}-1}}$ . Effectuer l'arrondi demande donc de faire ce calcul :

x.({\overline {2^{n}-1}})

Sur les ordinateurs qui utilisent le complètement à deux pour coder les nombres signés, cette expression se simplifie en :

x.(-2^{n})

Arrondi au multiple supérieur

Pour arrondir au multiple de x immédiatement supérieur, on peut procéder de différentes façons. On peut arrondir au multiple inférieur, et ajouter $2^{n}$ . Une autre solution consiste à mettre les n bits de poids faible à 1 dans le nombre à arrondir, avant d'ajouter 1. Ainsi, pour arrondir un nombre X, je dois effectuer le calcul suivant :

[X+(2^{n}-1)]+1

Ce qui est équivalent à :

[X+(2^{n}-1)].{\overline {2^{n}-1}}

[X+(2^{n}-1)].(-2^{n})

Détection d'un débordement de puissance de deux

Comme vous le savez peut-être, certaines architectures demandent aux accès mémoire de respecter des contraintes d'alignement. Pour rappel, la mémoire est alors découpée en blocs dont la taille est égale à la largeur du bus de données. Quand on charge une donnée, il est préférable que celle-ci soit intégralement contenue dans un bloc : l'accès mémoire est alors dit aligné. Si une donnée est à cheval sur deux blocs, elle devra alors être chargée en deux fois, ou causera une exception matérielle. Certains processeurs ne gèrent que des accès mémoires alignés. Pour diverses raisons, il est possible pour un programmeur de détecter si un accès mémoire sera ou non aligné. Un problème similaire apparait lorsque l'on doit charger une donnée depuis la mémoire RAM, sur les systèmes à mémoire virtuelle. Cette fois-ci, la mémoire virtuelle divise la RAM en pages, les données pouvant être à cheval sur deux pages. Détecter de tels chevauchements est alors une nécessité pour le système d’exploitation. Il se trouve qu'aussi bien la taille des pages que la largeur des blocs de RAM alignés sont des puissances de deux. Détecter les débordements de page ou de bloc alignés demande alors détecter quand une donnée est à cheval entre deux blocs de taille égale à $2^{n}$ . La donnée à charger commence à une adresse que nous noterons $A$ et a une longueur $L$ . Un débordement de page/bloc a lieu quand il existe un multiple de $2^{n}$ entre $A$ et $A+L$ : cela traduit le fait que la donnée commence dans un premier bloc, atteint la limite du bloc (donc, une adresse multiple de $2^{n}$ ) et se poursuit au-delà. Reste à voir comment les opérations bit à bit nous aident pour détecter une telle situation.

Méthode sans débordement d'entier

Pour cela, il existe deux solutions différentes, la première étant plus simple à comprendre que l'autre. La première demande se base sur le fait que l'adresse $A$ peut-être ou non un nombre divisible par la puissance de deux concernée. En clair, on sait que c'est un nombre de la forme $A=n\times 2^{n}+r_{0}$ . Un débordement a lieu si, en ajoutant $L$ , on passe au multiple suivant. En clair, un débordement a lieu si $A+L=(n+1)\times 2^{n}+r_{2}$ . En faisant quelques manipulations algébriques (soustraire A des deux côtés), cette condition se traduit alors en : $L+r_{0}>2^{n}$ . La logique est simple : si la longueur dépasse ce qu'il manque à l'adresse pour atteindre le prochain multiple de $2^{n}$ , alors l'adresse dépassera cette puissance : c'est un débordement. On peut alors faire le calcul assez simplement, vu que le reste $r_{0}=A\%2^{n}$ . Le calcul total est le suivant :

(A\%2^{n})+L>=2^{n}

On peut alors utiliser la méthode pour calculer le modulo par la puissance de deux :

\left[A|-(2^{n})\right]+L>=2^{n}

Méthode avec débordement d'entier

Une seconde méthode effectue un calcul similaire, si ce n'est qu'il arrive à remplacer la comparaison par un débordement d'entier. Le principe est très simple et se contente de remplacer l'adresse par le multiple de $2^{n}$ le plus grand possible qui soit adressable. Prenons par exemple une mémoire de 2^32 adresses, adressée par des adresses de 32 bits, découpée en page de 4096 octets. On suppose aussi que la machine travaille sur les mots/registres de 32 bits, comme les adresses. L'adresse la plus élevée, $2^{32}-1$ , n'est pas un multiple de 4096. L'adresse la plus grande multiple de 4096 est de 4294963200. Si à cette adresse on ajoute $L+A\%2^{n}$ , un débordement se produit si $L+A\%2^{n}>4096$ . En clair, le débordement d'entier traduit un débordement de page. On détecte donc un débordement de page si :

4294963200+L+(A\%2^{n})>2^{32}

Il se trouve que le calcul de $4294963200+(A\%2^{n})$ peut se réaliser sans faire l'addition. Tout ce qu'il faut faire est de remplacer les bits de poids forts de l'adresse par des 1, sans toucher aux bits sélectionnés par le modulo. L'application d'un masque est alors obligatoire, ce qui donne le code suivant :

(A|4294963200)+L>2^{32}

Ou encore :

(A|-4096)+L>2^{32}

On peut bien sûr généraliser les résultats précédents à toute autre valeur. Pour des adresses de $n$ bits et des pages/blocs de $m$ octets, on a :

(A|-m)+L>2^{n}

Puissance de deux immédiatement supérieure

Supposons que je veuille arrondir un nombre à puissance de deux immédiatement supérieure. Par exemple, je veux arrondir 5 à 8. Ou 25 à 32. Ou encore 250 à 256. Effectuer ce calcul peut sembler compliqué, si on ne prend pas le problème par le bon bout. Mais il y a une méthode asse simple pour faire ce calcul : il suffit de calculer non pas la puissance de deux, mais le nombre qui précède et de l'incrémenter. Le calcul de cette valeur, à savoir le nombre de la forme $2^{n}-1$ immédiatement supérieur, est en effet très simple à faire.

Pour cela, partons de l’exemple d'un nombre, que l'on va nommer N. Dans ce qui va suivre, ce N vaudra 0010 1101, pour l'exemple. Comme vous le voyez, ce nombre est de la forme 001X XXXX, avec X qui vaut zéro ou 1 selon le bit. Le nombre de la forme $2^{n}-1$ immédiatement supérieur lui, vaut 0011 1111. On voit que pour obtenir ce nombre, il faut recopier le 1 le plus à gauche, dans tous les bits à sa droite. Pour cela, quelques décalages font l'affaire. Pour vous donner une idée, regardons ce que vaut N OU (N >> 1) : 001X XXXX OR 0001 XXXX = 0011 XXXX. On voit que le 1 le plus à gauche a été recopié dans le bit à sa droite. Ensuite, regardons ce que vaut N OU (N >> 1) OU (N >> 2) : 001X XXXX OR 0001 XXXX OR 0000 1XXX = 0011 1XXX. Vous commencez à comprendre ? Les bits qui sont à droite du 1 le plus à gauche se remplissent progressivement avec des 1, au fur et à mesure des décalages. Si on pousse le bouchon encore plus loin, on se retrouvera avec un nombre dont tous les bits à droite du 1 le plus à gauche seront tous des 1. Le résultat est un nombre de la forme $2^{n}-1$ . Pour être plus précis, il s'agit du nombre de la forme $2^{n}-1$ . Il n'y a plus qu'à l'incrémenter pour obtenir la puissance de deux immédiatement supérieure.

On doit donc effectuer suffisamment de décalages pour mettre à 1 tous les bits à droite. On peut croire que pour un nombre de n bits, il faut effectuer n décalages. Mais en réalité, on peut réduire ce nombre assez facilement. Prenons l'exemple du nombre de la forme 1XXX XXXX. On peut effectuer un premier décalage d'un rang vers la droite, ce qui donne : 11XX XXXX. Ensuite, on peut prendre les deux bits à 1 et les recopier dans les deux bits qui suivent. C'est plus rapide que de remplir les bits par un par un. Il faut alors faire un décalage de deux rangs, ce qui donne : 1111 XXXX. Enfin, on peut recopier les 4 bits à 1 dans les 4 bits suivants, ce qui demande un décalage par 4. Si le nombre était plus long, on pourrait réutiliser la même logique : à chaque étape, le nombre de rangs pour le décalage double. Et cela marche pour tous les nombres, peu importe leur écriture binaire. Le code correspondant, bien qu'un petit peu amélioré et spécifique aux nombres de 32 bits, est le suivant :

unsigned NextPowerOf2 (unsigned n)
{
    n--;
    n |= n >> 1;
    n |= n >> 2;
    n |= n >> 4;
    n |= n >> 8;
    n |= n >> 16;
    return n++;
}

La décrémentation au début du code sert à gérer le cas où le nombre traité est lui-même une puissance de deux.

Cet article est issu de Wikibooks. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.