Dans ce chapitre et les suivants, nous allons voir comment implémenter sous forme de circuits certaines opérations extrêmement courantes dans un ordinateur. Les quelques circuits que nous allons voir seront réutilisés massivement dans les chapitres qui suivront, aussi nous allons passer quelque temps sur ces bases. Le présent chapitre abordera des opérations qui ne sont pas arithmétiques (comprendre des additions, multiplications ou autres), et qui portent le nom d’opérations logiques. Les opérations logiques travaillent sur des suites de bits d'une longueur fixe, l'écriture binaire d'un nombre pour simplifier. Il en existe de deux types, les instructions bit à bit et les instructions de décalage/rotation, mais ce chapitre se concentre sur les opérations bit à bit.
Les opérations bit à bit appliquent un ET, OU, XOR ou NOT sur un ou deux nombres. La plus simple est clairement l'opération NOT, qui inverse tous les bits d'un nombre : les 0 deviennent des 1, et les 1 deviennent des 0. Mais il est aussi possible de prendre deux nombres, de faire un ET/OU/XOR entre les bits de même poids, et de renvoyer le tout en guise de résultat. Le résultat de ces opérations n'est pas vraiment interprétable mathématiquement, la seule exception tient dans l'opération NOT.
- Pour un entier en complément à 1, le NOT sert à obtenir l'opposé d'un nombre : dit autrement, .
- Pour un entier en complément à deux, le NOT donne l'opposé d'un nombre auquel on aurait retranché 1 : .
- Pour un entier non-signé, le NOT va donner la valeur
Le premier point est une définition, c'est comme cela qu'on définit l'inverse d'un nombre en complément à un.
Le second point s'explique par le fait qu'en complément à deux, on a
Le dernier résultat est facile à comprendre quand on sait que la somme donne un nombre de n bits dont tous les bits sont à 1, égal par définition à .
Le circuit de calcul bit à bit
Dans ce qui va suivre, nous allons créer un circuit qui effectue toutes les opérations bit à bit possible avec deux bits. Divers théorèmes de l’algèbre de Boole nous disent que ces opérations sont au nombre de 16. Les traditionnels ET, OU, XOR, NAND, NOR et NXOR sont bien sûr comptés dans ces 16 opérations. Voici la liste complète de ces opérations, avec leur table de vérité ci-dessous (le nom des opérations n'est pas indiqué) :
- Les opérateurs nommés 0 et 1, qui renvoient systématiquement 0 ou 1 quel que soit l'entrée ;
- L'opérateur OUI qui recopie l'entrée a ou b, et l'opérateur non qui l'inverse : , , , ;
- L’opérateur ET, avec éventuellement une négation des opérandes : , , , ;
- La même chose avec l’opérateur OU : , , , ;
- Et enfin les opérateurs XOR et NXOR : , .
| a | b | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | - | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | - | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | - | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | - | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
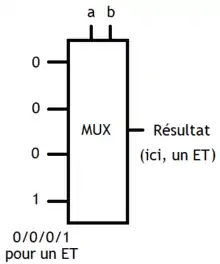
Le circuit à concevoir prend deux bits, que nous noterons a et b, et fournit sur sa sortie : soit a ET b, soit a OU b, soit a XOR b, etc. Pour sélectionner l'opération, une entrée du circuit indique quelle est l'opération à effectuer, chaque opération étant codée par un nombre. On pourrait penser que concevoir ce circuit serait assez complexe, mais il n'en est rien grâce à une astuce particulièrement intelligente. Regardez le tableau ci-dessus : vous voyez que chaque colonne forme une suite de bits, qui peut être interprétée comme un nombre. Il suffit d'attribuer ce nombre à l'opération de la colonne ! En faisant ainsi, le nombre attribué à chaque opération contient tous les résultats de celle-ci. Il suffit de sélectionner le bon bit parmi ce nombre pour obtenir le résultat. Et on peut faire cela avec un simple multiplexeur !
Il faut noter que le raisonnement peut se généraliser avec 3, 4, 5 bits, voire plus ! Et cela a déjà été utilisé sur de vrais ordinateurs.
Les masques
Il est possible d'utiliser les opérations bit à bit dans un grand nombre de situations, certes assez atypiques pour ce qui est du logiciel. Dans ce qui va suivre, nous allons voir comment modifier un bit dans un nombre, sans toucher aux autres. Pour donner un exemple d'utilisation, supposons que j'ai regroupé plusieurs bits, dont chacun a une signification bien précise. Par exemple, je peux regrouper les droits d'accès dans un fichier dans un nombre : un des bits du nombre me dira alors si je peux écrire dans le fichier, un autre me dira si je peux le lire, un autre si… Bref, si jamais je veux modifier mes droits en écriture de mon fichier, je dois mettre un bit bien précis à 1 ou à 0 (suivant la situation). Cela peut se faire facilement en utilisant une instruction bit à bit entre ce nombre et une constante bien choisie.
Un autre cas typique est celui où un développeur compacte plusieurs données dans un seul entier. Par exemple, prenons le cas d'une date, exprimée sous la forme jour/mois/année. Un développeur normal stockera cette date dans trois entiers : un pour le jour, un pour le mois, et un pour la date. Mais un programmeur plus pointilleux sera capable d'utiliser un seul entier pour stocker le jour, le mois, et l'année. Pour cela, il raisonnera comme suit :
- un mois comporte maximum 31 jours : on doit donc encoder tous les nombres compris entre 1 et 31, ce qui peut se faire en 5 bits ;
- une année comporte 12 mois, ce qui tient dans 4 bits ;
- et enfin, en supposant que l'on doive gérer les années depuis la naissance de Jésus jusqu'à l'année 2047, 11 bits peuvent suffire.
Dans ces conditions, notre développeur décidera d'utiliser un entier de 32 bits pour le stockage des dates :
- les 5 bits de poids forts serviront à stocker le jour ;
- les 4 bits suivant stockeront le mois ;
- et les bits qui restent stockeront l'année.
Dans cette situation, le développeur qui souhaite modifier le jour ou le mois d'une date devra modifier une partie des bits, tout en laissant les autres intacts. Encore une fois, cela peut se faire facilement en utilisant une instruction bit à bit entre ce nombre et une constante bien choisie.
L'opération OU bit à bit
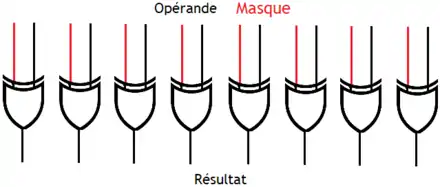
Tout d'abord, nous allons voir comment mettre à 1 un bit dans un nombre. Pour cela, nous allons utiliser une opération bit à bit entre le nombre en question, et un nombre appelé masque qui indique les bits à mettre à 1. Si le bit du masque est à 0, cela signifie que le bit du nombre, situé à la même place, ne doit pas être modifié. Mais si le bit du masque est à 1, le bit du nombre devra être mis à 1. Par exemple, pour modifier le 4éme bit d'un nombre en partant de la droite, le masque est une constante dont le 4éme bit en partant de la droite est 1, et le reste des bits est à 0, soit la constante : 000000001000.
Nous allons devoir trouver quelle opération bit à bit convient. Rien de compliqué au demeurant : il suffit d'écrire la table de vérité de cette opération et de reconnaitre la porte logique.
| Nombre | Masque | Résultat |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
On remarque que l’opération bit à bit à effectuer est un OU.
L'opération ET bit à bit
Mettre un bit à 0 dans un nombre fonctionne sur le même principe que mettre un bit à 1 : on effectue une opération bit à bit entre le nombre en question et un masque qui indique quels bits mettre à 0. Encore une fois, écrire la table de vérité de l'opération nous donne l'opération bit à bit à effectuer. Il s’avère que c'est un ET bit à bit.
| Nombre | Masque | Résultat |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
L'inverseur commandable
Dans cette section, nous allons voir un inverseur commandable, un circuit qui, comme son nom l'indique, inverse tout ou une partie des bits d'un nombre passé en entrée.
L'inverseur commandable par un bit d'inversion
Dans sa version la plus simple, ce circuit inverse un nombre quand on lui demande et ne fait rien sinon. On précise au circuit s'il doit inverser ou non l'opérande d'entrée avec un bit de commande, souvent nommé Invert. Ce dernier vaut 1 si le circuit doit inverser l'opérande et 0 sinon. Le circuit en question est assez simple à concevoir et se conçoit un peu comme les circuits de masquage vus juste au-dessus. L’opération est appliquée indépendamment pour chaque bit de l'opérande, ce qui fait que le circuit est composé d'un circuit d'inversion commandable par bit. On peut établir la table de ce circuit d'inversion qui prend un bit d'opérande et le bit de commande en entrée et fournit le bit de résultat en sortie. La table de vérité de ce circuit donne ceci :
| Bit de l’opérande | Bit de commande | Résultat |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
On voit que cette table de vérité est celle de l'opération XOR. Le circuit d'inversion commandable est donc composé d'une couche de portes XOR, chaque porte ayant une entrée connectée au bit de commande.
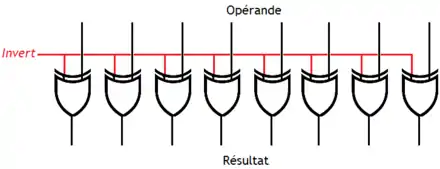
L'inverseur commandable par un masque
Il est possible d'améliorer le circuit précédent de manière à ce que seuls certains bits de l'entrée soient inversés. Pour préciser les bits à inverser, on peut utiliser un masque, comme vu plus haut pour ce qui est de mettre à 1 ou 0 certains bits d'un nombre. Les bits à 1 du masque indiquent qu'il faut inverser les bits de même poids dans l'entrée. Le masque est présenté en entrée du circuit et est appliqué sur l'entrée, donnant le résultat partiellement inversé. Le circuit n'est pas différent, si ce n'est que les entrées des portes XOR sont reliés non pas à une entrée Invert unique, mais au bit d'entrée du masque adéquat.