Dans le chapitre précédent, nous avons vu que les ordinateurs actuels utilisent un codage binaire. Ce codage binaire ne vous est peut-être pas familier. Aussi, dans ce chapitre, nous allons apprendre comment coder des nombres en binaire. Nous allons commencer par le cas le plus simple : les nombres positifs. Par la suite, nous aborderons les nombres négatifs. Et nous terminerons par les nombres à virgules, appelés aussi nombres flottants.
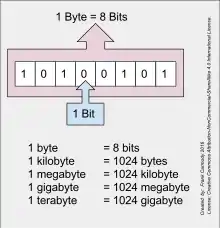
Mais avant toute chose, nous devons parler des regroupements de bits. En informatique, il n'est pas rare que l'on fasse usage de bits seuls, pour coder une information. Mais force est de constater que dans la plupart des cas, l'ordinateur manipule des nombres qui sont codés sur plusieurs bits. Les informaticiens ont donné des noms aux groupes de bits suivant leur taille. Le plus connu est certainement l'octet, qui désigne un groupe de 8 bits. Moins connu, on utilise aussi le terme de nibble pour parler d'un demi-octet, à savoir un groupe de 4. On parle aussi de doublet pour un groupe de 16 bits (deux octets) et de quadruplet pour un groupe de 32 bits (quatre octets). Précisons qu'en anglais, le terme byte a un double sens : il est utilisé pour désigner un octet, mais aussi un autre concept orthogonal que nous verrons plus tard (la plus petite unité de mémoire que le processeur peut adresser). Attention donc aux confusions. Dans ce cours, nous avons bien fait attention à parler d'octet pour désigner un groupe de 8 bits, en réservant le terme byte pour sa seconde signification.
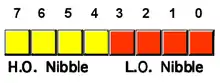 Nibbles dans un octet. |
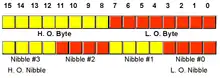 Octets et nibbles dans un doublet. |
Le codage des nombres entiers positifs
Pour coder des nombres entiers positifs, il existe plusieurs méthodes : le binaire, l’hexadécimal, le code Gray et le décimal codé binaire. La plus connue est certainement le binaire, secondée par l'hexadécimal, les deux autres étant plus anecdotiques. Pour comprendre ce qu'est le binaire, il nous faut faire un rappel sur les nombres entiers tel que vous les avez appris en primaire, à savoir les entiers écrits en décimal. Prenons un nombre écrit en décimal : le chiffre le plus à droite est le chiffre des unités, celui à côté est pour les dizaines, suivi du chiffre des centaines, et ainsi de suite. Dans un tel nombre :
- on utilise une dizaine de chiffres, de 0 à 9 ;
- chaque chiffre est multiplié par une puissance de 10 : 1, 10, 100, 1000, etc. ;
- la position d'un chiffre dans le nombre indique par quelle puissance de 10 il faut le multiplier : le chiffre des unités doit être multiplié par 1, celui des dizaines par 10, celui des centaines par 100, et ainsi de suite.
Exemple avec le nombre 1337 :
Pour résumer, un nombre en décimal s'écrit comme la somme de produits, chaque produit multipliant un chiffre par une puissance de 10. On dit alors que le nombre est en base 10.
Ce qui peut être fait avec des puissances de 10 peut être fait avec des puissances de 2, 3, 4, 125, etc : n'importe quel nombre entier strictement positif peut servir de base. En informatique, on utilise rarement la base 10 à laquelle nous sommes tant habitués. On utilise à la place deux autres bases :
- La base 2 (système binaire) : les chiffres utilisés sont 0 et 1 ;
- La base 16 (système hexadécimal) : les chiffres utilisés sont 0, 1, 2, 3, 4, 5, 6, 7, 8 et 9 ; auxquels s'ajoutent les six premières lettres de notre alphabet : A, B, C, D, E et F.
Le système binaire
En binaire, on compte en base 2. Cela veut dire qu'au lieu d'utiliser des puissances de 10 comme en décimal, on utilise des puissances de deux : n'importe quel nombre entier peut être écrit sous la forme d'une somme de puissances de 2. Par exemple 6 s'écrira donc 0110 en binaire : . On peut remarquer que le binaire n'autorise que deux chiffres, à savoir 0 ou 1 : ces chiffres binaires sont appelés des bits (abréviation de Binary Digit). Pour simplifier, on peut dire qu'un bit est un truc qui vaut 0 ou 1. Pour résumer, tout nombre en binaire s'écrit sous la forme d'un produit entre bits et puissances de deux de la forme :
Les coefficients sont les bits, l'exposant n qui correspond à un bit a_n est appelé le poids du bit. Le bit de poids faible est celui qui est le plus à droite du nombre, alors que le bit de poids fort est celui non nul qui est placé le plus à gauche.


Petite remarque assez importante : avec bits, on peut coder valeurs différentes, dont le , ce qui fait qu'on peut compter de à . N'oubliez pas cette petite remarque : elle sera assez utile dans la suite de ce tutoriel.
Traduction binaire->décimal
Pour traduire un nombre binaire en décimal, il faut juste se rappeler que la position d'un bit indique par quelle puissance il faut le multiplier. Ainsi, le chiffre le plus à droite est le chiffre des unités : il doit être multiplié par 1 (2^0). Le chiffre situé immédiatement à gauche du chiffre des unités doit être multiplié par 2 (2^1). Le chiffre encore à gauche doit être multiplié par 4 (2^2), et ainsi de suite. Mathématiquement, on peut dire que le énième bit en partant de la droite doit être multiplié par . Par exemple, la valeur du nombre noté 1011 en binaire est de (8×1)+(4×0)+(2×1)+(1×1) = 11.

Traduction décimal->binaire
La traduction inverse, du décimal au binaire, demande d'effectuer des divisions successives par deux. Les divisions en question sont des divisions euclidiennes, avec un reste et un quotient. En lisant les restes des divisions dans un certain sens, on obtient le nombre en binaire. Voici comment il faut procéder, pour traduire le nombre 34 :

La numérotation des bits
Il existe deux façons différentes de numéroter les bits. Ces numéros n'ont pas de rapport avec le poids du bit mais avec l'ordre de transmission bit par bit.
Exemple sur un octet (groupe de 8 bits) :
 |
Convention de numérotation LSB0 : Le premier bit transmis (bit 0) est celui de poids faible (LSB)
|
 |
Convention de numérotation MSB0 : Le premier bit transmis (bit 0) est celui de poids fort (MSB)
|
L'hexadécimal
L’hexadécimal est basé sur le même principe que le binaire, sauf qu'il utilise les 16 chiffres suivants :
| Chiffre hexadécimal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Nombre décimal correspondant | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| Notation binaire | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
Dans les textes, afin de différencier les nombres décimaux des nombres hexadécimaux, les nombres hexadécimaux sont suivis par un petit h, indiqué en indice. Si cette notation n'existait pas, des nombres comme 2546 seraient ambigus : on ne saurait pas dire sans autre indication s'ils sont écrits en décimal ou en hexadécimal. Avec la notation, on sait de suite que 2546 est en décimal et que 2546h est en hexadécimal.
Dans les codes sources des programmes, la notation diffère selon le langage de programmation.
Certains supportent le suffixe h pour les nombres hexadécimaux, d'autres utilisent un préfixe 0x ou 0h.
Traduction hexadécimal<->décimal
Pour convertir un nombre hexadécimal en décimal, il suffit de multiplier chaque chiffre par la puissance de 16 qui lui est attribué. Là encore, la position d'un chiffre indique par quelle puissance celui-ci doit être multiplié : le chiffre le plus à droite est celui des unités, le second chiffre le plus à droite doit être multiplié par 16, le troisième chiffre en partant de la droite doit être multiplié par 256 (16 * 16) et ainsi de suite. La technique pour convertir un nombre décimal vers de l’hexadécimal est similaire à celle utilisée pour traduire un nombre du décimal vers le binaire. On retrouve une suite de divisions successives, mais cette fois-ci les divisions ne sont pas des divisions par 2 : ce sont des divisions par 16.
Traduction hexadécimal<->binaire
La conversion entre hexadécimal et binaire est très simple, nettement plus simple que les autres conversions. Pour passer de l'hexadécimal au binaire, il suffit de traduire chaque chiffre en sa valeur binaire, celle indiquée dans le tableau au tout début du paragraphe nommé « Hexadécimal ». Une fois cela fait, il suffit de faire le remplacement. La traduction inverse est tout aussi simple : il suffit de grouper les bits du nombre par 4, en commençant par la droite (si un groupe est incomplet, on le remplit avec des zéros). Il suffit alors de remplacer le groupe de 4 bits par le chiffre hexadécimal qui correspond.
Le Binary Coded Decimal
Le Binary Coded Decimal, abrévié BCD, est une représentation qui mixe binaire et décimal. Elle était utilisée sur les tout premiers ordinateurs pour faciliter le travail des programmeurs. Avec cette représentation, les nombres sont écrits en décimal, comme nous en avons l'habitude dans la vie courante. Simplement, chaque chiffre décimal est directement traduit en binaire : au lieu d'utiliser les symboles 0, 1, 2, 3, 4, 5, 6, 7, 8 et 9, on codera chaque chiffre décimal sur quatre bits, en binaire normal. Par exemple, le nombre 624 donnera : 0110 0010 0100.
| Nombre encodé (décimal) | BCD | |||
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 |
| 6 | 0 | 1 | 1 | 0 |
| 7 | 0 | 1 | 1 | 1 |
| 8 | 1 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 |
On peut remarquer que quelques combinaisons de quatre bits ne sont pas des chiffres valides : c'est le cas des suites de bits qui correspondent à 10, 11, 12, 13, 14 ou 15. Ces combinaisons peuvent être utilisées pour représenter d'autres symboles, comme un signe + ou - afin de gérer les entiers relatifs, ou une virgule pour gérer les nombres non-entiers. Mais sur d'autres ordinateurs, ces combinaisons servaient à représenter des chiffres en double : ceux-ci correspondaient alors à plusieurs combinaisons.
Le code Gray
Avec le code Gray, deux nombres consécutifs n'ont qu'un seul bit de différence. Pour construire ce code Gray, on peut procéder en suivant plusieurs méthodes, les deux plus connues étant la méthode du miroir et la méthode de l'inversion.
Méthode du miroir
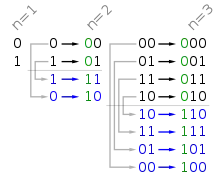
La méthode du miroir est relativement simple. Pour connaitre le code Gray des nombres codés sur n bits, il faut :
- partir du code Gray sur n-1 bits ;
- symétriser verticalement les nombres déjà obtenus (comme une réflexion dans un miroir) ;
- rajouter un 0 au début des anciens nombres, et un 1 au début des nouveaux nombres.
Il suffit de connaitre le code Gray sur 1 bit pour appliquer la méthode : 0 est codé par le bit 0 et 1 par le bit 1.
Méthode de l'inversion
Une autre méthode pour construire la suite des nombres en code Gray sur n bits est la méthode de l'inversion. Celle-ci permet de connaitre le codage du nombre n à partir du codage du nombre n-1, comme la méthode du dessus. On part du nombre 0, systématiquement codé avec uniquement des zéros. Par la suite, on décide quel est le bit à inverser pour obtenir le nombre suivant, avec la règle suivante :
- si le nombre de 1 est pair, il faut inverser le dernier chiffre.
- si le nombre de 1 est impair, il faut localiser le 1 le plus à droite et inverser le chiffre situé à sa gauche.
Pour vous entrainer, essayez par vous-même avec 2, 3, voire 5.
Interlude propédeutique : les débordements d'entiers
Dans la section précédente, nous avons vu comment coder des entiers positifs en binaire ou dans des représentations proches. La logique voudrait que l'on aborde ensuite le codage des entiers négatifs. Mais nous allons déroger à cette logique simple, pour des raisons pédagogiques. Avant de passer aux nombres négatifs, nous allons faire un interlude qui introduira des notions utiles pour la suite. Ces notions permettront d'introduire les notions nécessaires pour comprendre le complément à un et à deux. De plus, ces concepts seront abordés de nombreuses fois dans ce wikilivre et l'introduire ici est de loin une solution idéale. Voyons donc maintenant ce que sont les débordements d'entiers (integer overflow en anglais).
Les débordements d'entier
Tout ordinateur manipule des entiers de taille fixe, dont le nombre de bits est toujours le même. Pour les nombres positifs, un ordinateur qui code ses entiers sur n bits pourra coder tous les entiers allant de 0 à . Tout nombre en dehors de cet intervalle ne peut pas être représenté. Mais on peut imaginer d'autres codages pour lesquels les entiers ne commencent pas à zéro ou ne terminent pas à . On peut prendre le cas où l'ordinateur gère les nombres négatifs, par exemple. Dans le cas général, l'ordinateur peut coder les valeurs comprises de à . Si le résultat d'un calcul sort de cet intervalle, il ne peut pas être représenté par l'ordinateur et il se produit ce qu'on appelle un débordement d'entier.
La valeur haute de débordement désigne la première valeur qui est trop grande pour être représentée par l'ordinateur. Par exemple, pour un ordinateur qui peut coder tous les nombres entre 0 et 7, la valeur haute de débordement est égale à 8. On peut aussi définir la valeur basse de débordement, qui est la première valeur trop petite pour être codée par l'ordinateur. Par exemple, pour un ordinateur qui peut coder tous les nombres entre 8 et 250, la valeur basse de débordement est égale à 7. Pour les nombres entiers, la valeur haute de débordement vaut , alors que la valeur basse vaut (avec et respectivement la plus grande et la plus petite valeur codable par l'ordinateur).
La gestion des débordements d'entiers

Face à un débordement d'entier, l'ordinateur peut utiliser deux méthodes : l'arithmétique saturée ou l'arithmétique modulaire.
- L'arithmétique saturée consiste à arrondir le résultat au plus grand entier supporté par l'ordinateur si le résultat dépasse la valeur haute de débordement, ou au plus petit entier si la valeur basse est dépassée. La même chose est possible lors d'une soustraction, quand le résultat est inférieur à la plus petite valeur possible : l'ordinateur arrondit au plus petit entier possible.
- L'arithmétique modulaire est plus compliquée et c'est elle qui va nous intéresser dans ce qui suit. Pour simplifier, imaginons que l'on décompte à partir de zéro. Quand on arrive à la valeur haute de débordement, on recommence à compter à partir de zéro. L'arithmétique modulaire n'est pas si contre-intuitive et vous l'utilisez sans doute au quotidien. Après tout, c'est comme cela que l'on compte les heures, les minutes et les secondes. Quand on compte les minutes, on revient à 0 au bout de 60 minutes. Pareil pour les heures : on revient à zéro quand on arrive à 24 heures. Divers compteurs mécaniques fonctionnent sur le même principe et reviennent à zéro quand ils dépassent la plus grande valeur possible, l'image ci-contre en montrant un exemple.
Mathématiquement, l'arithmétique modulaire implique des divisions euclidiennes, celles qui donnent un quotient et un reste. Lors d'un débordement, le résultat s'obtient comme suit : on divise le nombre qui déborde par la valeur haute de débordement, et que l'on conserve le reste de la division. Au passage, l'opération qui consiste à faire une division et à garder le reste au lieu du quotient est appelée le modulo. Prenons l'exemple où l'ordinateur peut coder tous les nombres entre 0 et 1023, soit une valeur haute de débordement de 1024. Pour coder le nombre 4563, on fait le calcul 4563 / 1024. On obtient : . Le reste de la division est de 467 et c'est lui qui sera utilisé pour coder la valeur de départ, 4563. Le nombre 4563 est donc codé par la valeur 467 dans un tel ordinateur en arithmétique modulaire. Au passage, la valeur haute de débordement est toujours codée par un zéro dans ce genre d'arithmétique.
Les ordinateurs utilisent le plus souvent une valeur haute de débordement de , avec n le nombre de bits utilisé pour coder les nombres entiers positifs. En faisant cela, l'opération modulo devient très simple et revient à éliminer les bits de poids forts au-delà du énième bit. Concrètement, l'ordinateur ne conserve que les n bits de poids faible du résultat : les autres bits sont oubliés. Par exemple, reprenons l'exemple d'un ordinateur qui code ses nombres sur 4 bits. Imaginons qu'il fasse le calcul , soit 1101 + 0011 = 1 0000 en binaire. Le résultat entraîne un débordement d'entier et l'ordinateur ne conserve que les 4 bits de poids faible. Cela donne : 1101 + 0011 = 0000. Comme autre exemple l'addition 1111 + 0010 ne donnera pas 17 (1 0001), mais 1 (0001).
Les nombres entiers négatifs

Passons maintenant aux entiers négatifs en binaire : comment représenter le signe moins ("-") avec des 0 et des 1 ? Eh bien, il existe plusieurs méthodes :
- la représentation en signe-valeur absolue ;
- la représentation en complément à un ;
- la représentation en complément à deux;
- la représentation par excès ;
- la représentation dans une base négative ;
- d'autres représentations encore moins utilisées que les autres.
La représentation en signe-valeur absolue
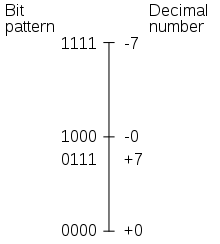
La solution la plus simple pour représenter un entier négatif consiste à coder sa valeur absolue en binaire, et rajouter un bit qui précise si c'est un entier positif ou un entier négatif. Par convention, ce bit de signe vaut 0 si le nombre est positif et 1 s'il est négatif. Avec cette technique, l'intervalle des entiers représentables sur N bits est symétrique : pour chaque nombre représentable en représentation signe-valeur absolue, son inverse l'est aussi. Ce qui fait qu'avec cette méthode, le zéro est codé deux fois : on a un -0, et un +0. Cela pose des problèmes lorsqu'on demande à notre ordinateur d'effectuer des calculs ou des comparaisons avec zéro.
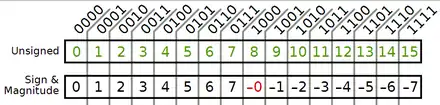
La représentation par excès
La représentation par excès consiste à ajouter un biais aux nombres à encoder afin de les encoder par un entier positif. Pour encoder tous les nombres compris entre -X et Y en représentation par excès, il suffit de prendre la valeur du nombre à encoder, et de lui ajouter un biais égal à X. Ainsi, la valeur -X sera encodée par zéro, et toutes les autres valeurs le seront par un entier positif. Par exemple, prenons des nombres compris entre -127 et 128. On va devoir ajouter un biais égal à 127, ce qui donne :
| Valeur avant encodage | Valeur après encodage |
|---|---|
| -127 | 0 |
| -126 | 1 |
| -125 | 2 |
| … | … |
| 0 | 127 |
| … | … |
| 127 | 254 |
| 128 | 255 |
Les représentations en complément à un et en complément à deux
Les représentations en complément à un et en complément à deux sont deux représentations basées sur le même principe. Leur idée est de remplacer chaque nombre négatif par un nombre positif équivalent, appelé le complément. Par équivalent, on veut dire que les résultats de tout calcul reste le même si on remplace le nombre négatif initial par son complément. Et pour faire cela, elles se basent sur les débordements d'entier pour fonctionner, et plus précisément sur l'arithmétique modulaire abordée plus haut. Si on fait les calculs avec le complément, les résultats du calcul vont entrainer un débordement d'entier, qui sera résolu par un modulo. Et le résultat après modulo sera identique au résultat qu'on aurait obtenu avec le nombre négatif sans modulo. En clair, c'est la gestion des débordements qui permet de corriger le résultat de manière à ce que l'opération avec le complément donne le même résultat qu'avec le nombre négatif voulu. Ainsi, on peut coder un nombre négatif en utilisant son complément positif.
La différence entre complément à un et à deux tient dans la valeur haute de débordement. Pour des nombres codés sur bits, la valeur haute de débordement est égale à en complément à deux, alors qu'elle est de en complément à un. De ce fait, la gestion des débordements est plus simple en complément à deux. Concrètement, lors d'un débordement d'entier, l'ordinateur ne conserve que les bits de poids faible du résultat : les autres bits sont oubliés. Par exemple, reprenons l'addition 13 + 3 vue précédemment. En binaire, cela donne : 1101 + 0011 = 1 0000. En ne gardant que les 4 bits de poids faible, on obtient : 1101 + 0011 = 0000. Comme autre exemple l'addition 1111 + 0010 ne donnera pas 17 (10001), mais 1 (0001).
Le calcul du complément
Voyons maintenant comment convertir un nombre décimal en représentation en complément. Précisons que la procédure de conversion est différente suivant que le nombre est positif ou négatif. Pour les nombres positifs, il suffit de les traduire en binaire, sans faire quoi que ce soit de plus. C'est pour les nombres négatifs que la procédure est différente et qu'il faut calculer le complément. La méthode pour déterminer le complément est assez simple. Prenons par exemple un codage sur 4 bits dont la valeur haute de débordement est de 16. Prenons l'addition de 13 + 3 = 16. Avec l'arithmétique modulaire, 16 est équivalent à 0, ce qui donne : 13 + 3 = 0 ! On peut aussi reformuler en disant que 13 = -3, ou encore que 3 = -13. Dit autrement, 3 est le complément de -13 pour ce codage. Et ne croyez pas que ça marche uniquement dans cet exemple : cela se généralise assez rapidement à tout nombre négatif.
Prenons un nombre négatif N et son complément à deux K. Dans ce qui suit, les additions modulo n seront notées comme suit : . La notation se généralise aux autres opérations. Dans le cas général, on a :
Si on fait le calcul sur l'ordinateur, on obtient :
On peut donc calculer le complément d'un nombre comme suit :
Ce qui donne, respectivement en complément à deux et à un :
Pour le complément à un, on peut simplifier le calcul assez fortement. En effet, la valeur est par définition un nombre dont tous les bits sont à 1. A cette valeur, on soustrait un nombre dont certains bits sont à 1 et d'autres à 0. Or, les règles de l'arithmétique binaire, que nous aborderons dans un futur chapitre, nous disent que et . En regardant attentivement, on se rend compte que le bit du résultat est l'inverse du bit de départ. En clair, le complément à un s'obtient en codant la valeur absolue en binaire, puis en inversant tous les bits du résultat (les 0 se transforment en 1 et réciproquement). On a donc :
Pour le complément à deux, on peut utiliser le même raisonnement. Pour cela, reprenons l'équation précédente :
Elle peut se réécrire comme suit :
Or, : n'est autre que le complément à un, ce qui donne :
En clair, le complément à deux s'obtient en prenant le complément à un et en ajoutant 1. Dit autrement, il faut prendre le nombre N, en inverser tous les bits et ajouter 1.
Comparaison entre complément à un et à deux
Avec le complément à un, le zéro est codé deux fois, avec un zéro positif et un zéro négatif. Les calculs sont cependant légèrement plus simples qu'en complément à deux, notamment quand il faut calculer le complément. Remarquez qu'en complément à un, la valeur haute de débordement est le zéro négatif. Traduire en décimal un nombre en complément à un est assez facile : il suffit de le traduire comme on le ferait avec du binaire non-signé, mais en ne tenant pas compte du bit de poids fort. Le signe du résultat est indiqué par le bit de poids fort : 1 pour un nombre négatif et 0 pour un nombre positif.
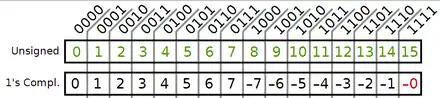
Avec le complément à deux, le zéro n'est codé que par un seul nombre binaire. Le zéro négatif est remplacé par une valeur négative, par la plus petite valeur négative pour être précis. C'est un avantage suffisant pour que tous les ordinateurs utilisent cette représentation. Pour savoir quelle est la valeur décimale d'un entier en complément à deux, on utilise la même procédure que pour traduire un nombre du binaire vers le décimal, à un détail près : le bit de poids fort (celui le plus à gauche) doit être multiplié par la puissance de deux associée, mais le résultat doit être soustrait au lieu d'être additionné.
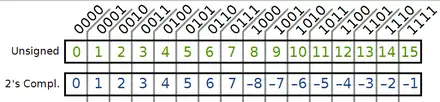
- Avec les deux représentations, le bit de poids fort vaut 0 pour les nombres positifs et 1 pour les négatifs : il agit comme un bit de signe.
L'extension de signe
Dans nos ordinateurs, tous les nombres sont codés sur un nombre fixé et constant de bits. Ainsi, les circuits d'un ordinateur ne peuvent manipuler que des nombres de 4, 8, 12, 16, 32, 48, 64 bits, suivant la machine. Si l'on veut utiliser un entier codé sur 16 bits et que l'ordinateur ne peut manipuler que des nombres de 32 bits, il faut bien trouver un moyen de convertir notre nombre de 16 bits en un nombre de 32 bits, sans changer sa valeur et en conservant son signe. Cette conversion d'un entier en un entier plus grand, qui conserve valeur et signe s'appelle l'extension de signe. L'extension de signe des nombres positifs consiste à remplir les bits de poids fort avec des 0 jusqu’à arriver à la taille voulue : c'est la même chose qu'en décimal, où rajouter des zéros à gauche d'un nombre positif ne changera pas sa valeur. Pour les nombres négatifs, il faut remplir les bits à gauche du nombre à convertir avec des 1, jusqu'à obtenir le bon nombre de bits : par exemple, 1000 0000 (-128 codé sur 8 bits) donnera 1111 1111 1000 000 après extension de signe sur 16 bits. L'extension de signe d'un nombre codé en complément à 2 se résume donc en une phrase : il faut recopier le bit de poids fort de notre nombre à convertir à gauche de celui-ci jusqu’à atteindre le nombre de bits voulu.
La représentation négabinaire
Enfin, il existe une dernière méthode, assez simple à comprendre, appelée représentation négabinaire. Dans cette méthode, les nombres sont codés non en base 2, mais en base -2. Oui, vous avez bien lu : la base est un nombre négatif. Dans les faits, la base -2 est similaire à la base 2 : il y a toujours deux chiffres (0 et 1), et la position dans un chiffre indique toujours par quelle puissance de 2 il faut multiplier, sauf qu'il faudra ajouter un signe moins une fois sur 2. Concrètement, les puissances de -2 sont les suivantes : 1, -2, 4, -8, 16, -32, 64, etc. En effet, un nombre négatif multiplié par un nombre négatif donne un nombre positif, ce qui fait que une puissance sur deux est négative, alors que les autres sont positives. Ainsi, on peut représenter des nombres négatifs, mais aussi des nombres positifs dans une puissance négative.
Par exemple, la valeur du nombre noté 11011 en base -2 s'obtient comme suit :
| … | -32 | 16 | -8 | 4 | -2 | 1 |
|---|---|---|---|---|---|---|
| … | 1 | 1 | 1 | 0 | 1 | 1 |
Sa valeur est ainsi de (−32×1)+(16×1)+(−8×1)+(4×0)+(−2×1)+(1×1)=−32+16−8−2+1=−25.
Les nombres à virgule
On sait donc comment sont stockés nos nombres entiers dans un ordinateur. Néanmoins, les nombres entiers ne sont pas les seuls nombres que l'on utilise au quotidien : il nous arrive d'en utiliser à virgule. Notre ordinateur n'est pas en reste : il est lui aussi capable de manipuler de tels nombres. Dans les grandes lignes, il peut utiliser deux méthodes pour coder des nombres à virgule en binaire : La virgule fixe et la virgule flottante.
Les nombres à virgule fixe
La méthode de la virgule fixe consiste à émuler les nombres à virgule à partir de nombres entiers. Un nombre à virgule fixe est codé par un nombre entier proportionnel au nombre à virgule fixe. Pour obtenir la valeur de notre nombre à virgule fixe, il suffit de diviser l'entier servant à le représenter par le facteur de proportionnalité. Par exemple, pour coder 1,23 en virgule fixe, on peut choisir comme « facteur de conversion » 1000, ce qui donne l'entier 1230.
Généralement, les informaticiens utilisent une puissance de deux comme facteur de conversion, pour simplifier les calculs. En faisant cela, on peut écrire les nombres en binaire et les traduire en décimal facilement. Pour l'exemple, cela permet d'écrire des nombres à virgule en binaire comme ceci : 1011101,1011001. Et ces nombres peuvent se traduire en décimal avec la même méthode que des nombres entier, modulo une petite différence. Comme pour les chiffres situés à gauche de la virgule, chaque bit situé à droite de la virgule doit être multiplié par la puissance de deux adéquate. La différence, c'est que les chiffres situés à droite de la virgule sont multipliés par une puissance négative de deux, c'est à dire par , , , , , ...
Cette méthode est assez peu utilisée de nos jours, quoiqu'elle puisse avoir quelques rares applications relativement connue. Un bon exemple est celui des banques : les sommes d'argent déposées sur les comptes ou transférées sont codés en virgule fixe. Cela permet de gérer le cas des centimes sans problèmes : il suffit d'utiliser un facteur de conversion égal à 100. Dit autrement, les sommes manipulées par les ordinateurs ne sont pas exprimées en euros, mais en centimes d'euros. La raison de ce choix est que les autres méthodes de codage des nombres à virgule peuvent donner des résultats imprécis : il se peut que les résultats doivent être tronqués ou arrondis, suivant les opérandes. Cela n'arrive jamais en virgule fixe, du moins quand on se limite aux additions et soustractions.
Les nombres flottants
Les nombres à virgule fixe ont aujourd'hui été remplacés par les nombres à virgule flottante, où le nombre de chiffres après la virgule est variable. De nos jours, les ordinateurs utilisent un standard pour le codage des nombres à virgule flottante : la norme IEEE 754. Avec cette norme, l'écriture d'un nombre flottant est basée sur son écriture scientifique. Pour rappel, en décimal, l’écriture scientifique d'un nombre consiste à écrire celui-ci comme un produit entre un nombre et une puissance de 10, de la forme . Le nombre ne possède qu'un seul chiffre à gauche de la virgule : on peut toujours trouver un exposant tel que ce soit le cas. En base 10, sa valeur est comprise entre 1 (inclus) et 10 (exclu). En binaire, c'est la même chose, mais avec une puissance de deux. L'écriture scientifique binaire d'un nombre consiste à écrire celui-ci sous la forme . Le nombre ne possède toujours qu'un seul chiffre à gauche de la virgule, comme en base 10. Vu qu'en binaire, seuls deux chiffres sont possibles (0 et 1), le chiffre de a situé à gauche de la virgule est soit un zéro ou un 1.
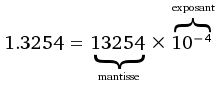
Pour stocker cette écriture scientifique, il faut donc stocker : la partie fractionnaire du nombre , qu'on appelle la mantisse, l'exposant de la puissance de deux et un bit de signe. Pour les nombres flottants, le bit à gauche de la virgule vaut 1, sauf dans quelques rares exceptions que nous aborderons plus tard. On verra que ce bit peut se déduire en fonction de l'exposant utilisé pour encoder le nombre à virgule, ce qui lui vaut le nom de bit implicite. L'exposant peut être aussi bien positif que négatif (pour permettre de coder des nombres très petits), et est encodé en représentation par excès sur n bits avec un biais égal à .

Les formats de nombres flottants
Les flottants doivent être stockés dans la mémoire d'une certaine façon, standardisée par la norme. Cette norme va (entre autres) définir quatre types de flottants différents, qui pourront stocker plus ou moins de valeurs différentes.
| Classe de nombre flottant | Nombre de bits utilisés pour coder un flottant | Nombre de bits de l'exposant | Nombre de bits pour la mantisse | Décalage |
|---|---|---|---|---|
| Simple précision | 32 | 8 | 23 | 127 |
| Double précision | 64 | 11 | 52 | 1023 |
| Double précision étendue | 80 ou plus | 15 ou plus | 64 ou plus | 16383 ou plus |
IEEE754 impose aussi le support de certains nombres flottants spéciaux qui servent notamment à stocker des valeurs comme l'infini. Commençons notre revue des flottants spéciaux par les dénormaux, aussi appelés flottants dénormalisés. Ces flottants ont une particularité : leur bit implicite vaut 0. Ces dénormaux sont des nombres flottants où l'exposant est le plus petit possible. Le zéro est un dénormal particulier dont la mantisse est nulle. Au fait, remarquez que le zéro est codé deux fois à cause du bit de signe : on se retrouve avec un -0 et un +0.
| Bit de signe | Exposant | Mantisse |
|---|---|---|
| 0 ou 1 | Valeur minimale (0 en binaire) | Mantisse différente de zéro (dénormal strict) ou égale à zéro (zéro) |
Fait étrange, la norme IEEE754 permet de représenter l'infini, aussi bien en positif qu'en négatif. Celui-ci est codé en mettant l'exposant à sa valeur maximale et la mantisse à zéro. Et le pire, c'est qu'on peut effectuer des calculs sur ces flottants infinis. Mais cela a peu d'utilité.
| Bit de signe | Exposant | Mantisse |
|---|---|---|
| 0 ou 1 | Valeur maximale | Mantisse égale à zéro |
Mais malheureusement, l'invention des flottants infinis n'a pas réglé tous les problèmes. Par exemple, quel est le résultat de ? Ou encore ? Autant prévenir tout de suite : mathématiquement, on ne peut pas savoir quel est le résultat de ces opérations. Pour pouvoir résoudre ces calculs, il a fallu inventer un nombre flottant qui signifie « je ne sais pas quel est le résultat de ton calcul pourri ». Ce nombre, c'est NaN. NaN est l'abréviation de Not A Number, ce qui signifie : n'est pas un nombre. Ce NaN a un exposant dont la valeur est maximale, mais une mantisse différente de zéro. Pour être plus précis, il existe différents types de NaN, qui diffèrent par la valeur de leur mantisse, ainsi que par les effets qu'ils peuvent avoir. Malgré son nom explicite, on peut faire des opérations avec NaN, mais cela ne sert pas vraiment à grand chose : une opération arithmétique appliquée avec un NaN aura un résultat toujours égal à NaN.
| Bit de signe | Exposant | Mantisse |
|---|---|---|
| 0 ou 1 | Valeur maximale | Mantisse différente de zéro |
Les arrondis et exceptions
La norme impose aussi une gestion des arrondis ou erreurs, qui arrivent lors de calculs particuliers. En voici la liste :
| Nom de l’exception | Description |
|---|---|
| Invalid operation | Opération qui produit un NAN. Elle est levée dans le cas de calculs ayant un résultat qui est un nombre complexe, ou quand le calcul est une forme indéterminée. Pour ceux qui ne savent pas ce que sont les formes indéterminées, voici en exclusivité la liste des calculs qui retournent NaN : , , , , . |
| Overflow | Résultat trop grand pour être stocké dans un flottant. Le plus souvent, on traite l'erreur en arrondissant le résultat vers Image non disponible ; |
| Underflow | Pareil que le précédent, mais avec un résultat trop petit. Le plus souvent, on traite l'erreur en arrondissant le résultat vers 0. |
| Division par zéro | Le nom parle de lui-même. La réponse la plus courante est de répondre + ou - l'infini. |
| Inexact | Le résultat ne peut être représenté par un flottant et on doit l'arrondir. |
La gestion des arrondis pose souvent problème. Pour donner un exemple, on va prendre le nombre 0,1. En binaire, ce nombre s'écrit comme ceci : 0,1100110011001100... et ainsi de suite jusqu'à l'infini. Notre nombre utilise une infinité de décimales. Bien évidemment, on ne peut pas utiliser une infinité de bits pour stocker notre nombre et on doit impérativement l'arrondir. Comme vous le voyez avec la dernière exception, le codage des nombres flottants peut parfois poser problème : dans un ordinateur, il se peut qu'une opération sur deux nombres flottants donne un résultat qui ne peut être codé par un flottant. On est alors obligé d'arrondir ou de tronquer le résultat de façon à le faire rentrer dans un flottant. Pour éviter que des ordinateurs différents utilisent des méthodes d'arrondis différentes, on a décidé de normaliser les calculs sur les nombres flottants et les méthodes d'arrondis. Pour cela, la norme impose le support de quatre modes d'arrondis :
- Arrondir vers + l'infini ;
- vers - l'infini ;
- vers zéro ;
- vers le nombre flottant le plus proche.
Les nombres flottants logarithmiques
Les nombres flottants logarithmiques sont une spécialisation des nombres flottants IEEE754, ou tout du moins une spécialisation des flottants écrits en écriture scientifique. Avec ces nombres logarithmiques, la mantisse est totalement implicite : tous les flottants logarithmiques ont la même mantisse, qui vaut 1. Seul reste l'exposant, qui varie suivant le nombre flottant. On peut noter que cet exposant est tout simplement le logarithme en base 2 du nombre encodé, d'où le nombre de codage flottant logarithmique donné à cette méthode. Un nombre logarithmique est donc composé d'un bit de signe et d'un exposant, sans mantisse. Attention toutefois : l'exposant est ici un nombre fractionnaire, ce qui signifie qu'il est codé en virgule fixe. Le choix d'un exposant fractionnaire permet de représenter pas mal de nombres de taille diverses.
| Bit de signe | Exposant | |
|---|---|---|
| Représentation binaire | 0 | 01110010101111 |
| Représentation décimale | + | 1040,13245464 |
L'utilité de cette représentation est de simplifier certains calculs, comme les multiplications, divisions, puissances, etc. En effet, les mathématiques de base nous disent que le logarithme d'un produit est égal à la somme des logarithmes : . Or, il se trouve que les ordinateurs sont plus rapides pour faire des additions/soustractions que pour faire des multiplications/divisions. On verra dans quelques chapitres que les circuits électroniques d'addition/soustraction sont beaucoup plus simples que les circuits pour multiplier et/ou diviser. Dans ces conditions, la représentation logarithmique permet de remplacer les multiplications/divisions par des opérations additives plus simples et plus rapides pour l'ordinateur. Évidemment, les applications des flottants logarithmiques sont rares, limitées à quelques situations bien précises (traitement d'image, calcul scientifique spécifiques).