Cosmologie/Le destin de l'univers

Dans les chapitres précédents, nous avons établit les deux équations de Friedmann. Pour rappel, les voici :

H^{2}={\frac {8\pi G}{3c^{2}}}\rho _{e}-{\frac {k\cdot c^{2}}{a^{2}}}+{\frac {\Lambda c^{2}}{3}}

{\frac {a''}{a}}={\frac {\Lambda c^{2}}{3}}-{\frac {4\pi G}{3c^{2}}}(\rho _{e}+3P)

On peut déduire bien des choses à partir de ces équations, notamment comment le facteur de Hubble évolue avec la densité et comment il varie au cours du temps. Cela nous permet de déduire ce qu'il adviendra de l'univers. Continuera-t-il à s'étendre indéfiniment ? Ou au contraire, l'expansion cessera-t-elle au bout d'un certain temps ? L'univers finira-t-il par s'effondrer sur lui-même ? Il n'y a pas 36 possibilités et seuls trois scénarios sont possibles :

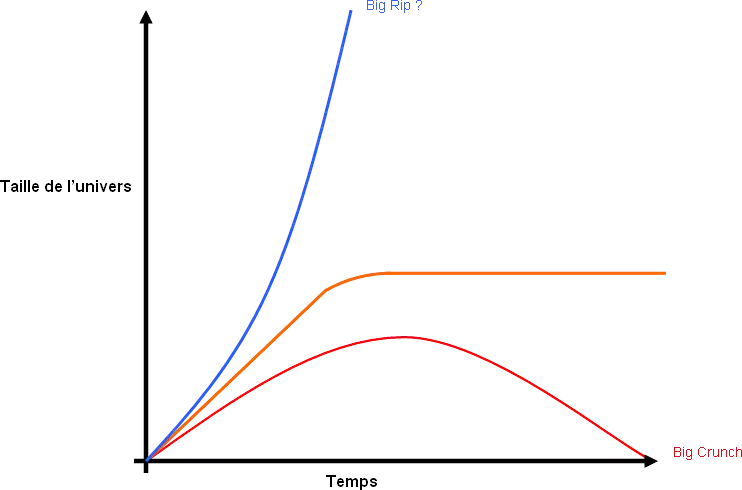
Dans le premier scénario, l'expansion de l'univers finit par cesser et s'inverse, l'univers se contracte et le volume de l'univers observable diminue. En clair, l'univers s'effondre sur lui-même dans un grand big-crunch.
Dans le second cas, l'expansion de l'univers ne s’arrête jamais et ne ralentit pas (soit qu'elle reste stable, soit que l'expansion accélère). Dans ce cas, l'univers grossit indéfiniment : c'est le scénario du big-rip.
Et enfin, dans le dernier scénario, l'expansion de l'univers ne s’arrête jamais, mais celle-ci ralentit progressivement. L'univers commence par s'étendre, mais son rythme de croissance diminue peu à peu, jusqu’à s'annuler après un temps infini. Dans ce scénario, l'univers ne grossit pas indéfiniment et verra son volume tendre progressivement vers un volume maximum. Ce scénario est appelé le big chill.

Trois possibilités pour l'évolution de l'univers.

Le lien avec le facteur de Hubble et de facteur d'échelle

Le scénario qui se matérialise dépend du facteur de Hubble. Rappelons en effet que le facteur de Hubble est le taux d'expansion de l'univers, le taux auquel l'univers augmente de volume. Un H négatif signifie que l'univers se contracte, un H positif signifie que l'univers est en expansion, et un H nul signifie que l'univers est stationnaire. Pour l'étude du destin de l'univers, on se préoccupe du facteur de Hubble obtenu après un temps assez long, pour un âge de l'univers très important. Idéalement, on doit étudier la limite de H quand le temps tend vers l'infini : $\lim _{t\rightarrow \infty }H(t)$ . On distingue les trois scénarios précédents selon que la limite de H est positive, négative ou nulle.

Positive : l'expansion de l'univers ne s’arrête jamais et c'est le big rip qui se matérialise.
Nulle : le big chill se matérialise si la limite tend vers 0.
Négative : l'expansion s'inverse si la limite devient négative et l'univers finit en big-crunch.

Il est aussi possible de voir les choses à partir du facteur d'échelle, en utilisant la dérivée du facteur d'échelle. Quand ${\frac {da}{dt}}>0$ , le facteur d'échelle augmente au cours du temps, ce qui implique un univers en expansion. Par contre, ${\frac {da}{dt}}<0$ implique un facteur d'échelle qui se réduit au cours du temps et donc un univers qui se contracte. Enfin, ${\frac {da}{dt}}=0$ implique un univers stable, qui n'est ni en expansion ni en contraction.

En théorie, on devrait étudier le destin de l'univers, ce qui veut dire son état quand l'âge de l'univers est très avancé, voire à la limite $t\rightarrow \infty$ . Mais les équations précédentes sont écrites avec le facteur d'échelle, pas avec le temps. Cependant, le facteur d'échelle dépend du temps et on peut l'utiliser en remplacement, sous certaines hypothèses.

Dans le cas du big crunch, l'univers gonfle avant de se rétracter. Au niveau du facteur d'échelle, cela signifie que le facteur d'échelle est initialement croissant, cesse de croître à un temps bien précis, et décroît au-delà. Au niveau du facteur de Hubble, cela signifie qu'il est d'abord positif (univers en expansion), puis s'annule, et enfin devient négatif. On est donc dans le cas où la dérivée du facteur d'échelle s'annule pour un temps fini.

Dans le cas du big chill, la dérivée s'annule, mais seulement pour la limite $t\rightarrow \infty$ . L'univers ne cesse de croître et ce n'est qu'après un temps infini qu'il se stabilise.

Dans le cas du big rip, la dérivée reste positive quand on passe à la limite $t\rightarrow \infty$ . L'univers ne cesse de croître et ne se stabilise pas, même après un temps infini.

	$\lim _{t\rightarrow \infty }\left({\frac {da}{dt}}\right)$	$\lim _{t\rightarrow \infty }a(t)$
Big Crunch	Négative	Nulle
Big Chill	Nulle	Infinie
Big Rip	Positive	Infinie

Le calcul de la dérivée du facteur d'échelle

On peut calculer la dérivée du facteur d'échelle en utilisant la formule $a'(t)={\frac {da}{dt}}$ . Et donc, on peut la calculer indirectement à partir de la première équation de Friedmann. Celle-ci s'écrit en effet, comme on l'a vu dans le chapitre sur l'énergie noire :

\left({\frac {da}{dt}}\right)^{2}=a^{2}\left[{\frac {8\pi G}{3c^{2}}}\rho _{e}+{\frac {\Lambda c^{2}}{3}}\right]-k\cdot c^{2}

Pour rappel, la densité d'énergie est égale à la densité de matière et la densité de rayonnement :

\left({\frac {da}{dt}}\right)^{2}=a^{2}\left[{\frac {8\pi G}{3c^{2}}}(\rho _{m}(t)+\rho _{r}(t))+{\frac {\Lambda c^{2}}{3}}\right]-k\cdot c^{2}

Pour rappel, la densité de matière et de rayonnement évoluent comme suit : $\rho _{m}(t)=\rho _{m}0\cdot a^{(}t){-3}$ et $\rho _{r}(t)=\rho _{r}0\cdot a(t)^{-4}$ . En injectant dans l'équation précédente, on a :

\left({\frac {da}{dt}}\right)^{2}=a^{2}\left[{\frac {8\pi G}{3c^{2}}}\left({\frac {\rho _{m}0}{a^{3}}}+{\frac {\rho _{r}0}{a^{4}}}\right)+{\frac {\Lambda c^{2}}{3}}\right]-k\cdot c^{2}

On simplifie :

\left({\frac {da}{dt}}\right)^{2}={\frac {8\pi G}{3c^{2}}}\left({\frac {\rho _{m}0}{a}}+{\frac {\rho _{r}0}{a^{2}}}\right)+a^{2}{\frac {\Lambda c^{2}}{3}}-k\cdot c^{2}

On prend alors la limite quand t tend vers l'infini :

\lim _{t\rightarrow \infty }\left({\frac {da}{dt}}\right)^{2}=\lim _{t\rightarrow \infty }\left[{\frac {8\pi G}{3c^{2}}}\left({\frac {\rho _{m}0}{a}}+{\frac {\rho _{r}0}{a^{2}}}\right)+a^{2}{\frac {\Lambda c^{2}}{3}}-k\cdot c^{2}\right]

En sortant les termes indépendants de t de la limite, on a :

\lim _{t\rightarrow \infty }\left({\frac {da}{dt}}\right)^{2}={\frac {8\pi G}{3c^{2}}}\left[\lim _{t\rightarrow \infty }\left({\frac {\rho _{m}0}{a}}+{\frac {\rho _{r}0}{a^{2}}}\right)\right]+{\frac {\Lambda c^{2}}{3}}\left[\lim _{t\rightarrow \infty }a^{2}\right]-k\cdot c^{2}

Le cas du big crunch

Dans le cas du big crunch, l'univers décroît au-delà d'un certain temps et se ratatine sur lui-même au point d'atteindre un volume nul. Traduit mathématiquement, cela se traduit par les équations suivantes :

\lim _{t\rightarrow \infty }a(t)=0

\lim _{t\rightarrow \infty }\left({\frac {da}{dt}}\right)^{2}<0

On part de l'équation des sections précédentes :

\lim _{t\rightarrow \infty }{\frac {da}{dt}}^{2}={\frac {8\pi G}{3c^{2}}}\left[\lim _{t\rightarrow \infty }\left({\frac {\rho _{m}0}{a}}+{\frac {\rho _{r}0}{a^{2}}}\right)\right]+{\frac {\Lambda c^{2}}{3}}\left[\lim _{t\rightarrow \infty }a^{2}\right]-k\cdot c^{2}

On combine les deux équations précédentes :

{\frac {8\pi G}{3c^{2}}}\left[\lim _{t\rightarrow \infty }\left({\frac {\rho _{m}0}{a}}+{\frac {\rho _{r}0}{a^{2}}}\right)\right]+{\frac {\Lambda c^{2}}{3}}\left[\lim _{t\rightarrow \infty }a^{2}\right]-k\cdot c^{2}<0

On réorganise :

{\frac {8\pi G}{3c^{2}}}\left[\lim _{t\rightarrow \infty }\left({\frac {\rho _{m}0}{a(t)}}+{\frac {\rho _{r}0}{a(t)^{2}}}\right)\right]+{\frac {\Lambda c^{2}}{3}}\left[\lim _{t\rightarrow \infty }a(t)^{2}\right]<k\cdot c^{2}

Or, on a vu que le big crunch impliquait que : $\lim _{t\rightarrow \infty }a(t)=0$ . En injectant dans l'équation précédente, on trouve :

{\frac {8\pi G}{3c^{2}}}\left[\lim _{t\rightarrow \infty }\left({\frac {\rho _{m}0}{a(t)}}+{\frac {\rho _{r}0}{a(t)^{2}}}\right)\right]<k\cdot c^{2}

Cette inégalité nous dit que le big crunch n'est possible que si l'univers a une courbure positive et que celle-ci a une intensité suffisante. Il faut alors que l'effet de la constante cosmologique et de la gravité soient compensés quand l'âge de l'univers a atteint une valeur suffisante.

Le cas du big rip

Pour le big-rip, on a, par définition du big rip :

\lim _{t\rightarrow \infty }a(t)=\infty

.

\lim _{t\rightarrow \infty }{\frac {da}{dt}}>0

.

On part de l'équation des sections précédentes :

\lim _{t\rightarrow \infty }{\frac {da}{dt}}^{2}={\frac {8\pi G}{3c^{2}}}\left[\lim _{t\rightarrow \infty }\left({\frac {\rho _{m}0}{a}}+{\frac {\rho _{r}0}{a^{2}}}\right)\right]+{\frac {\Lambda c^{2}}{3}}\left[\lim _{t\rightarrow \infty }a^{2}\right]-k\cdot c^{2}

On combine les deux équations précédentes :

{\frac {8\pi G}{3c^{2}}}\left[\lim _{t\rightarrow \infty }\left({\frac {\rho _{m}0}{a}}+{\frac {\rho _{r}0}{a^{2}}}\right)\right]+{\frac {\Lambda c^{2}}{3}}\left[\lim _{t\rightarrow \infty }a^{2}\right]-k\cdot c^{2}>0

On réorganise :

{\frac {8\pi G}{3c^{2}}}\left[\lim _{t\rightarrow \infty }\left({\frac {\rho _{m}0}{a}}+{\frac {\rho _{r}0}{a^{2}}}\right)\right]+{\frac {\Lambda c^{2}}{3}}\left[\lim _{t\rightarrow \infty }a^{2}\right]>k\cdot c^{2}

On utilise alors la condition $\lim _{t\rightarrow \infty }a(t)=\infty$ . On en déduit que les facteurs ${\frac {\rho _{m}}{a(t)}}$ et ${\frac {\rho _{r}}{a(t)^{2}}}$ deviennent très petits, au point d'être négligeables, et vont s'annuler avec l'augmentation progressive de $a$ . On a alors :

{\frac {\Lambda c^{2}}{3}}\left[\lim _{t\rightarrow \infty }a^{2}\right]>k\cdot c^{2}

L'équation nous dit que la présence d'une constante cosmologique non-nulle suffit à elle seule pour que le big-rip survienne. Mais dans le cas où elle est nulle, le big rip dépend de la valeur de la courbure. Supposons que la constante cosmologique soit nulle, ce qui donne :

{\frac {0\cdot c^{2}}{3}}\left[\lim _{t\rightarrow \infty }a^{2}\right]>k\cdot c^{2}

Ce qui se simplifie en :

0>k\cdot c^{2}

On voit que le big rip est possible si $\lambda =0$ , mais à condition que la courbure soit négative.

Pour résumer, le big rip a lieu soit si la constante cosmologique est positive, soit si la courbure est négative (et même suffisamment négative pour compenser l'effet de la gravité/densité). Dit autrement, le destin de l'univers dépend uniquement de la valeur de la constante cosmologique et de la courbure.

Le cas du big chill

Dans le cas du big chill, le facteur d'échelle tend vers l'infini et sa dérivée tend vers zéro :

\lim _{t\rightarrow \infty }a(t)=\infty

.

\lim _{t\rightarrow \infty }{\frac {da}{dt}}=0

.

On part de l'équation des sections précédentes :

\lim _{t\rightarrow \infty }{\frac {da}{dt}}^{2}={\frac {8\pi G}{3c^{2}}}\left[\lim _{t\rightarrow \infty }\left({\frac {\rho _{m}0}{a}}+{\frac {\rho _{r}0}{a^{2}}}\right)\right]+{\frac {\Lambda c^{2}}{3}}\left[\lim _{t\rightarrow \infty }a^{2}\right]-k\cdot c^{2}

On combine les deux équations précédentes :

{\frac {8\pi G}{3c^{2}}}\left[\lim _{t\rightarrow \infty }\left({\frac {\rho _{m}0}{a}}+{\frac {\rho _{r}0}{a^{2}}}\right)\right]+{\frac {\Lambda c^{2}}{3}}\left[\lim _{t\rightarrow \infty }a^{2}\right]-k\cdot c^{2}=0

On réorganise :

{\frac {8\pi G}{3c^{2}}}\left[\lim _{t\rightarrow \infty }\left({\frac {\rho _{m}0}{a}}+{\frac {\rho _{r}0}{a^{2}}}\right)\right]+{\frac {\Lambda c^{2}}{3}}\left[\lim _{t\rightarrow \infty }a^{2}\right]=k\cdot c^{2}

On ajoute alors la contrainte $\lim _{t\rightarrow \infty }a(t)=\infty$ . Dans ce cas, on a $\lim _{t\rightarrow \infty }\left({\frac {\rho _{m}0}{a}}+{\frac {\rho _{r}0}{a^{2}}}\right)=0$ et $\lim _{t\rightarrow \infty }a^{2}=\infty$ . On a alors :

{\frac {\Lambda c^{2}}{3}}\left[\lim _{t\rightarrow \infty }a^{2}\right]=k\cdot c^{2}

Ce qui n'est possible que si la constante cosmologique est nulle, idem pour la courbure. Un univers en big chill ne peut atteindre un volume infini que si sa courbure et sa constante cosmologique sont toutes les deux nulles, en présence de matière et/ou de rayonnement.

Résumé

Dans les paragraphes précédents, on sait quel est le destin de l'univers en fonction de son contenu. Tout dépend de la valeur de la constante cosmologique et de sa courbure, la présence de matière et de rayonnement important peu. On peut donc résumer le tout dans un tableau à deux entrées, qui donne le destin de l'univers en fonction du signe de la courbure et de la constante cosmologique.

Courbure/ $\lambda$	Nulle	Positive
Négative	Big Rip	Big Rip
Nulle	Big chill	Big Rip
Positive	Big Crunch	Dépend de qui l'emporte

La densité critique et le paramètre de densité

Maintenant, étudions le cas d'un univers à courbure nulle et sans constante cosmologique. La première équation de Friedmann devient alors :

H^{2}={\frac {8\pi G}{3c^{2}}}\rho _{e}

On peut alors calculer la densité qui correspond, qui s'appelle la densité critique.

\rho _{c}={\frac {3H^{2}c^{2}}{8\pi G}}

La densité critique correspond à la densité d'un univers de courbure nulle. Vous remarquerez qu'il existe une valeur de densité différente pour chaque valeur de la constante de Hubble.

Les cosmologistes utilisent souvent le rapport entre la densité mesurée expérimentalement et la densité critique, ce rapport étant appelé le paramètre de densité. Celui-ci vaut, par définition :

\Omega ={\frac {\rho }{\rho _{c}}}={\frac {8\pi G}{3H^{2}c^{2}}}\cdot \rho

À partir de cette équation, on peut montrer que $\Omega -1$ est la déviation par rapport la densité critique, exprimée en proportion de la densité critique.

\Omega -1={\frac {\rho }{\rho _{c}}}-1={\frac {\rho -\rho _{c}}{\rho _{c}}}

Détermination de la courbure

Cette équation permet de déterminer la courbure de l'univers à partir du paramètre de densité. En effet, une fois le paramètre de densité connu, on peut alors en déduire quelle est la courbure via quelques manipulations algébriques sur l'équation précédente.

Pour cela, on part de l'équation de Friedmann sous cette forme :

H^{2}+{\frac {k\cdot c^{2}}{a^{2}}}={\frac {8\pi G}{3c^{2}}}\rho

On divise par $H^{2}$ :

1+{\frac {k\cdot c^{2}}{a^{2}H^{2}}}={\frac {8\pi G}{3c^{2}H^{2}}}\rho

Le terme de droite n'est autre que le rapport $\Omega ={\frac {8\pi G}{3H^{2}c^{2}}}\cdot \rho$ , par définition :

1+{\frac {k\cdot c^{2}}{a^{2}H^{2}}}=\Omega

Ce qui s'écrit aussi comme suit :

\Omega -1={\frac {k\cdot c^{2}}{a^{2}H^{2}}}

En multipliant par ${\frac {a^{2}H^{2}}{c^{2}}}$ , on a :

k={\frac {a^{2}H^{2}}{c^{2}}}(\Omega -1)

On injecte alors la formule $H={\frac {a'(t)}{a(t)}}$ :

k=\left[{\frac {a'(t)}{a(t)}}\right]^{2}{\frac {a^{2}}{c^{2}}}(\Omega -1)

On simplifie par $a^{2}$ :

k={\frac {1}{c^{2}}}{\frac {da(t)^{2}}{dt}}(\Omega -1)

Cette équation nous donne une interprétation du paramètre de courbure. Si celui-ci est égal à 1, la courbure de l'univers est nulle et la densité de l'univers est égale à la densité critique. Si il est positif, la densité de courbure est légèrement positive et réciproquement pour un paramètre de densité négatif. Le paramètre de densité peut se mesurer indirectement, via diverses observations astronomiques. On peut en effet mesurer avec précision le facteur de Hubble, ainsi que la densité de l'univers.

Évolution de l'univers

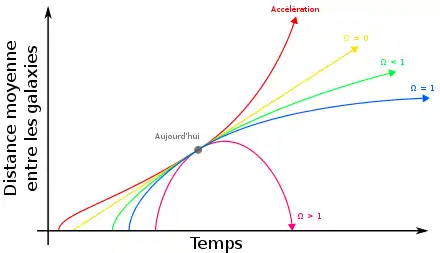
À l'heure actuelle, il semblerait que la courbure soit nulle, ou tout du moins tellement faible qu'on peut la considérer comme nulle. Toutes les mesures, réalisées par les satellites WMAP et Planck donnent bien une valeur quasiment nulle, aux imprécisions expérimentales près. Les mesures les plus récentes, provenant du satellite Planck, nous disent qu'il y a 95% de chances pour que le paramètre de densité soit compris entre 1.0008 et −1.0029.Aussi, dans les développements mathématiques des prochains chapitres, je supposerais que la courbure est nulle.

Reformulation de la première équation de Friedmann

Il est possible de reformuler la première équation de Friedmann avec ce paramètre de courbure. Cependant, cela demande de fournir différents paramètres de densité. En effet, il ne faut pas oublier l'influence différentielle du facteur d'échelle sur la matière, l'énergie de rayonnement et la courbure. Pour cela, il faut utiliser différents paramètres de densité : un pour la matière, un autre pour le rayonnement, et un autre pour la courbure. Le premier est égal à la densité de matière divisée par la densité critique et est noté $\Omega _{m}$ . Le second est égal à la densité de rayonnement divisée par la densité critique et est noté $\Omega _{r}$ . Même principe pour le rapport entre densité de courbure et densité critique $\Omega _{k}$ .

H(a)^{2}=H_{0}^{2}\left(\Omega _{k}a^{-2}+\Omega _{m}a^{-3}+\Omega _{r}a^{-4}\right)

Une autre formulation donne, si l'on considère l'énergie noire :

H(a)^{2}=H_{0}^{2}\left(\Omega _{k}a^{-2}+\Omega _{m}a^{-3}+\Omega _{r}a^{-4}+\Omega _{\Lambda }\right)

Cet article est issu de Wikibooks. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.